Функция распределения случайных величин. Непрерывные случайные величины
Функцией распределения СВ Х называется такая функция F(X), которая для каждого х выражает вероятность того, что СВ Х примет значение, меньшее х:
| F(x) = P(X < х). | (1.6) |
На рис. 1.2 дана функция распределения для ряда распределения из табл. 1.1. Пример формульного представления функции распределения:
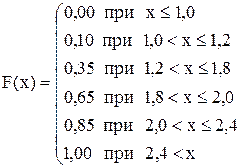
 F F
| ||||||||||||
| 1,0 | ||||||||||||
| 0,5 | ||||||||||||
| 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 | 2,4 | X |
Рис. 1.2. Пример функции распределения для дискретной СВ
Свойства функции распределения (ФР):
1. ФР СВ есть неотрицательная функция: 0 £ F(x) £ 1.
2. ФР СВ есть неубывающая функция: если х1< х2, то F(x1) £ F(x2)
3. F(-¥) = 0, F(+¥) = 1.
4. Вероятность попадания СВ Х в интервал [х1, х2) равна приращению ее ФР на этом интервале: Р(х1 £ Х < х2 ) = F(х2) - F(х1).
СВ Х называется непрерывной, если ее ФР непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек.
Плотность вероятности (распределения) j(х) непрерывной СВ есть производная ее ФР: j(х) = F’(x). Плотность вероятности существует только для непрерывных СВ.
Свойства плотности вероятности j(х) СВ Х:
1. j(х) неотрицательная функция: j(х) ³ 0.
2. Вероятность попадания непрерывной СВ в интервал [а,b]:
P(a £ X £ b) = 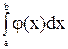 . .
| (1.7) | |
| 33. | F(x) = 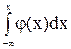 . .
| (1.8) |
| 44. | 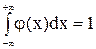 . .
| (1.9) |
Для непрерывной СВ Х МО и дисперсия определяются так:
а = М(Х) = 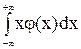 , ,
| (1.10) |
D(x) = 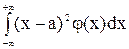 ,
или
D(x) = ,
или
D(x) = 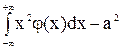 . .
| (1.11) |
Числовые характеристики СВ, включая МО, дисперсию, СКО, делятся на начальные nk и центральные mk моменты k-го порядка:
| для дискретных СВ: | |
nk = S 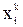 pi pi
| mk =S (xi - a)kpi, |
| для непрерывных СВ: | |
nk= 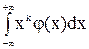
| mk= 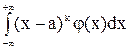 . .
|
Дата добавления: 2019-10-16; просмотров: 668;
