Точечные и интервальные оценки параметров
Оценкой 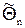 параметра Q называют всякую функцию от результатов над n наблюдениями СВ Х, посредством которой судят о значении параметра Q. Оценку
параметра Q называют всякую функцию от результатов над n наблюдениями СВ Х, посредством которой судят о значении параметра Q. Оценку 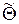 называют также статистикой.
называют также статистикой.
Если Q - величина детерминированная, то ее оценка 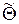 - случайная величина, которая в смысле качества оценивания может быть лучше или хуже. Качество оценивания определяется по трем критериям: несмещенность, состоятельность, эффективность.
- случайная величина, которая в смысле качества оценивания может быть лучше или хуже. Качество оценивания определяется по трем критериям: несмещенность, состоятельность, эффективность.
Оценка 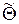 параметра Q называется несмещенной, если ее МО равно параметру Q:
параметра Q называется несмещенной, если ее МО равно параметру Q:
М( 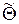 ) = Q. ) = Q.
| (1.36) |
Требование несмещенности гарантирует отсутствие систематических ошибок при оценивании.
Оценка 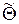 параметра Q называется состоятельной, если она удовлетворяет закону больших чисел, т.е. сходится по вероятности к Q:
параметра Q называется состоятельной, если она удовлетворяет закону больших чисел, т.е. сходится по вероятности к Q:
lim P(ê 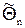 - Q ê £ e) = 1 при n®¥. - Q ê £ e) = 1 при n®¥.
| (1.37) |
Как видно, с увеличением объема n выборки значительные ошибки оценивания становятся все менее вероятными.
Оценка 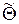 параметра Q называется эффективной, если она несмещенная и имеет наименьшую дисперсию среди всех возможных несмещенных оценок, вычисленных по выборкам одного объема n. Эффективность является решающим критерием качества оценивания, поскольку совмещает в себе два критерия.
параметра Q называется эффективной, если она несмещенная и имеет наименьшую дисперсию среди всех возможных несмещенных оценок, вычисленных по выборкам одного объема n. Эффективность является решающим критерием качества оценивания, поскольку совмещает в себе два критерия.
Основным методом получения оценок параметров по данным выборки является метод максимального правдоподобия. Согласно ему в качестве оценки 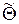 принимается такое ее значение, которое максимизирует функцию правдоподобия L:
принимается такое ее значение, которое максимизирует функцию правдоподобия L:
| L(x1, x2, ... , xn, Q) = P ji(xi, Q). | (1.38) |
Функция L есть плотность вероятности (вероятность) совместного появления данных выборки x1, x2, ... , xn, Получаемая из выражения Arg(L(x1, x2, ... , xn, Q) 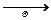 max) =
max) = 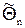 оценка такова, что имеющиеся у нас наблюдения являются наиболее правдоподобными.
оценка такова, что имеющиеся у нас наблюдения являются наиболее правдоподобными.
Достоинство метода максимального правдоподобия: получаемые с его помощью оценки состоятельны, асимптотически (при n®¥) эффективны и имеют асимптотически (при n®¥) нормальный ЗР.
Пусть имеется выборка x1, x2, ... , xn, по которой методом максимального правдоподобия оцениваются параметры распределения СВ Х. Тогда:
выборочная средняя 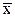 = ånixi/n,
= ånixi/n,
выборочная дисперсия s2 = åni(xi - 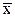 )2/n,
)2/n,
выборочная доля w=m/n.
Здесь 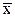 и w - несмещенные, состоятельные и эффективные (для нормально распределенной генеральной совокупности) оценки для МО а и вероятности р, а s2 - смещенная, но состоятельная оценка дисперсии s2.
и w - несмещенные, состоятельные и эффективные (для нормально распределенной генеральной совокупности) оценки для МО а и вероятности р, а s2 - смещенная, но состоятельная оценка дисперсии s2.
Обычно в качестве оценки используется исправленная выборочная дисперсия, которая является несмещенной и состоятельной оценкой дисперсии s2.
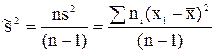 .
.
Мы рассмотрели точечные оценки параметров. Помимо них существуют интервальные оценки.
Интервальной оценкой параметра Q называется интервал ( 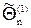 ,
, 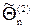 ), который с заданной вероятностью g накрывает неизвестное значение параметра Q. Интервал (
), который с заданной вероятностью g накрывает неизвестное значение параметра Q. Интервал ( 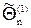 ,
, 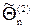 ) называется доверительным, а вероятность g - доверительной вероятностью (надежностью) оценки. Величина доверительного интервала уменьшается с ростом объема выборки n и растет с ростом доверительной вероятности g.
) называется доверительным, а вероятность g - доверительной вероятностью (надежностью) оценки. Величина доверительного интервала уменьшается с ростом объема выборки n и растет с ростом доверительной вероятности g.
Пример построения доверительного интервала. Пусть x1, x2, ... , xn, -выборка, полученная случайным отбором с повтором из генеральной совокупности с НЗР. Пусть 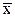 и
и 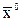 - средние выборочная и генеральная, s - выборочное СКО,
- средние выборочная и генеральная, s - выборочное СКО, 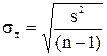 - СКО выборочной средней. Поскольку статистика (
- СКО выборочной средней. Поскольку статистика ( 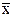 -
- 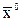 )/
)/ 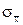 = (
= ( 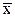 -
- 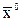 )
) 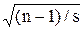 имеет t-распределение Стьюдента с n-1 степенями свободы, доверительный интервал для генеральной средней
имеет t-распределение Стьюдента с n-1 степенями свободы, доверительный интервал для генеральной средней 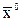 с доверительной вероятностью g будет таким:
с доверительной вероятностью g будет таким:
( 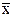 - tg, n-1 - tg, n-1 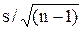 , , 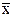 + tg, n-1 + tg, n-1 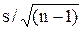 ). ).
| (1.39) |
Дата добавления: 2019-10-16; просмотров: 727;
