Проверка статистических гипотез
Статистической гипотезой называется любое предположение о свойстве параметра или неизвестного закона распределения. При этом возможны четыре исхода относительно основной - нулевой - гипотезы Но, (табл. 1.2) . Вероятность a допустить ошибку 1-го рода называется уровнем значимости критерия.
Таблица 1.2
| Гипотеза Но | Н0 принимается | Н0 отвергается |
| Но верна | Правильное решение | Ошибка 1-го рода (вероятность a) – уровень значимости критерия |
| Но неверна | Ошибка 2-го рода (вероятность b) | Правильное решение: вероятность 1-b есть мощность критерия |
Суть проверки гипотезы состоит в том, что используется статистика 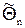 , полученная по выборке x1, x2, ... , xn . Затем по таблице определяется критическое значение Qкр такое, что если гипотеза Но верна, то вероятность Р(
, полученная по выборке x1, x2, ... , xn . Затем по таблице определяется критическое значение Qкр такое, что если гипотеза Но верна, то вероятность Р( 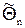 > Qкр) пренебрежимо мала. Поэтому, если обнаружится, что
> Qкр) пренебрежимо мала. Поэтому, если обнаружится, что 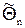 > Qкр, то Но отвергается. Если же
> Qкр, то Но отвергается. Если же 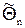 £ Qкр, то гипотеза Но принимается.
£ Qкр, то гипотеза Но принимается.
Вероятность 1-b не допустить ошибку 2-го рода называется мощностью критерия.
В зависимости от вида конкурирующей гипотезы Н1 (она является отрицанием гипотезы Но ) выбирают правостороннюю, левостороннюю или двустороннюю критическую область. Границы критической области при заданном a определяются из соотношений:
· для правосторонней критической области:
Р( 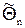 > Qкр) = a, > Qкр) = a,
| (1.40) |
· для левосторонней критической области:
Р( 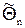 < Qкр) =a, < Qкр) =a,
| (1.41) |
· для двусторонней критической области:
Р( 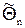 < Qкр.1) = Р( < Qкр.1) = Р( 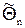 > Qкр.2) = a/2. > Qкр.2) = a/2.
| (1.42) |
Проверка статистической гипотезы не дает логического (дедуктивного) доказательства ее истинности или ложности. Принятие гипотезы Но является лишь правдоподобным, не противоречащим опыту утверждением – индуктивным доказательством.
Приложение 2
Дата добавления: 2019-10-16; просмотров: 498;
