Многомерные случайные величины и условные законы распределения
Упорядоченный набор Х= (X1, X2, ... , Xn ) случайных величин называется n-мерной СВ.
Функцией распределения n-мерной СВ (X1, X2, ... , Xn ) называется функция F(x1, x2, ... , xn), являющаяся вероятностью совместного выполнения n неравенств:
| F(x1, x2, ... , xn) = Р(Х1< х1, Х2< х2, ... , Хn< xn). | (1.23) |
Двумерная функция распределения:
| F(x, y) = Р(Х< х, Y< y). | (1.24) |
Свойства ФР F(x, y):
1. 0 £ F(x, y) £ 1.
2. Если x1 < x2, то F(x1, y) £ F(x2, y), аналогично и для y1 < y2 .
3. F(x, -¥) = F(-¥, y) = F(-¥,-¥) = 0.
4. F(x, ¥) = F1(x), F(¥, y) = F2(y), где F1(x) и F2(y) - функции распределения СВ Х и Y соответственно.
5. F(¥,¥) = 1.
Плотностью вероятности (совместной плотностью) непрерывной двумерной СВ (Х, Y) называется вторая смешанная частная производная ее ФР:
j(x, y) = Fxy”(x, y) = 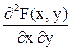
| (1.25) |
Свойства плотности вероятности двумерной СВ j(x, y):
1. j(x, y) ³ 0.
2. P((x, y) Î D) = 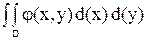 .
.
3. F(x, y) = 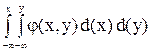 .
.
4. 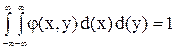 .
.
Условным ЗР СВ Х, взятой из двумерной СВ(Х, Y), называется закон распределения СВ Х, полученный при условии, что другая СВ Y приняла определенное значение. Условная плотность вероятности jy(x) двумерной СВ (Х, Y) определяется формулой:
jy(x) = 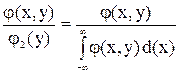 .
.
Числовые характеристики условного распределения: условное МО а(у)=Му(Х) и условная дисперсия s2(у)=Dy(X). Другие их обозначения: М(Хêу) и D(Хêу).
Условное МО СВ Y при Х=х, т.е. Мх(Y), есть функция от х, называемая функцией регрессии (регрессией) Y по Х.
Пример. Пусть двумерная СВ (Х, Y) и ее ЗР j(x, y) являются некоторой моделью железной дороги, причем СВ Х - количество порожних вагонов в суточной заявке порта, СВ Y - количество поставленных порожних вагонов за сутки в порт. Тогда регрессия Мх(Y) показывает соотношение между заявкой и поставкой вагонов в среднем (рис. 1.3).

| Мх(Y) (шт.) | 
| ||||||

| |||||||

| 
| ||||||

| |||||||

| 
| ||||||

| |||||||

| |||||||
| |||||||
| X (шт.) |
Рис. 1. 3
Свойства условного МО:
1. Если Z = z(X), где z - неслучайная функция от Х, то Mz(Mx(Y)) = =Mz(Y), в частности, М(Мх(Y)) = М(У).
2. Если Z = z(X), то Mz(Z×Y) - Z×Мх(Y).
3. Если СВ Х и Y независимы, то Мх(Y) = М(Y) (на рис. 1.3 это была бы горизонтальная прямая).
Для независимых СВ j(x, y) = j1(x)∙j2(y), или jу(x) = j1(x) и jх(y) = j2(y), где j1 и j2 - плотности одномерных СВ Х и Y, jу(x) и jх(y) - плотности условных распределений Х по Y и Y по Х.
Зависимость между двумя СВ называется статистической, если каждому значению одной из них соответствует определенное (условное) распределение другой.
Ковариацией (корреляционным моментом) Cov(Х, Y) СВ Х и Y называется МО произведения отклонений этих величин от своих МО:
| Cov(Х, Y) = М((Х-ах)( Y-ау)). | (1.26) |
Другие обозначения ковариации: Кху, 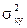 .
.
Ковариация двух СВ характеризует, во-первых, степень их взаимозависимости, во-вторых, их рассеяние вокруг точки (ах, ау).
Для измерения только тесноты связи двух СВ применяют безразмерный коэффициент корреляции r:
| r = Cov(Х, Y) / (sхsу). | (1.27) |
Свойства ковариации:
1. Cov(Х, Y) = 0, если Х и Y независимы.
2. Cov(Х, Y) = М(Х, Y) - ах ау.
3. êCov(Х, Y)ê £ sхsу.
Свойства коэффициента корреляции r:
1. -1 £ r £ 1.
2. r = 0, если СВ Х и Y независимы. Обратное утверждение неверно.
3. если êr ê = 1, то СВ Х и Y связаны линейной функциональной зависимостью.
Дата добавления: 2019-10-16; просмотров: 590;
