И тесты на ее наличие
В регрессионных моделях пространственных выборок отсутствует влияние предыдущих наблюдений на последующие. Как следствие - выполняется условие независимости возмущений: r(ei, ej)=0. Совсем другая картина наблюдается во временных выборках. Здесь предыдущее значение уровня ряда, как правило, оказывает значительное влияние на последующее значение. Примером может служить курс валют на завтра – основой для его формирования служит сегодняшний курс.
Соответствующие регрессионные модели называются моделями с наличием автокорреляции. Последняя может быть положительной (завтра вероятнее всего будет то же, что и сегодня - устойчивость) и отрицательной (завтра вероятнее всего будет совсем не то же, что сегодня - маятник).
Процессы с положительной автокорреляцией содержат низкочастотную периодическую составляющую (еженедельный пик торговли на рынке). Процессы с отрицательной автокорреляцией не содержат такой составляющей и больше похожи на "белый шум".
Обычный метод наименьших квадратов при наличии коррелированности ошибок регрессии дает несмещенные и состоятельные, но неэффективные оценки коэффициентов регрессии. Как итог - оценки их дисперсий несостоятельные и смещенные, что делает результаты тестирования гипотез недостоверными.
Как правило, при наличии автокорреляции наибольшее влияние на последующее значение оказывает предыдущее значение. Поэтому отсутствие корреляции между соседними членами ряда служит хорошим критерием того, что корреляция отсутствует вообще.
Тест Дарбина-Уотсона основан именно на такой идее. Нулевая гипотеза Но: автокореляция отсутствует. Критическая статистика Дарбина-Уотсона имеет вид:
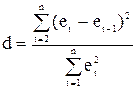 . .
| (6.19) |
Статистика d связана с выборочным коэффициентом корреляции (тем точнее, чем больше n):
| d » 2(1-r). | (6.20) |
При r=-1 d=4 (отрицательная автокорреляция), при r=0 d=2 (отсутствие автокорреляции), при r=+1 d=0 (положительная автокорреляция).
На рис. 6.3 изображена связь значения d-статистики с результатами тестирования для n>14 (dн и dв - нижняя и верхняя границы - находятся по таблицам):
1. dн <d<4- dв - гипотеза Но не отвергается (принимается).
2. dн <d<dв - гипотеза Но не отвергается и не принимается - область неопределенности критерия.
3. 0<d<dн - принимается альтернативная гипотеза о положительной автокорреляции.
4. 4-dн<d<4 - принимается альтернативная гипотеза об отрицательной автокорреляции.
| Но отвергается (положительная автокорреляция) | Зона неопределенности | Но принимается (отсутствие автокорреляции) | Зона неопределенности | Но отвергается (отрицательная автокорреляция) |
0 dн dв 2 4-dв 4-dн 4
Рис. 6.3. Схема теста Дарбина-Уотсона
Недостатки теста Дарбина-Уотсона: наличие зон неопределенности критерия, ограниченность результата - выявление корреляции только между двумя соседними членами ряда.
Тест Бреуша-Годфри основан на выражении корреляции между соседними наблюдениями авторегрессионным уравнением первого порядка:
| et = rе t-1 , t=1, 2, ... , n, | (6.21) |
где et - остатки регрессии, полученные обычным МНК.
Тест состоит в следующем: если коэффициент регрессии r значимо отличается от нуля, то автокорреляция имеет место.
Преимущества этого теста перед тестом Дарбина-Уотсона:
- не содержит зон неопределенностей;
- может измерять наличие автокорреляции не только между смежной парой возмущений, но и с учетом других возмущений: е t-2 , е t-3 . Для этого в уравнение (6.21) нужно ввести эти регрессоры.
Существуют и другие тесты.
Дата добавления: 2019-10-16; просмотров: 632;
