Признаки обобщенной линейной модели
Коренное отличие обобщенной модели от классической состоит только в виде ковариационной квадратной матрицы вектора возмущений: вместо матрицы åe=s2Еn для классической модели имеем матрицу åe=W для обобщенной. Последняя имеет произвольные значения ковариаций и дисперсий. Например, ковариационные матрицы классической и обобщенной моделей для двух наблюдений (n=2) в общем случае будут иметь вид:
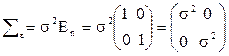 ,
,
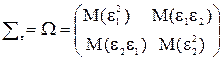 .
.
Формально обобщенная линейная модель множественной регрессии (ОЛММР) в матричной форме имеет вид:
| Y = Xb + e | (6.1) |
и описывается системой условий:
1. e - случайный вектор возмущений с размерностью n; Х - неслучайная матрица значений объясняющих переменных (матрица плана) с размерностью nx(p+1); напомним, что 1-й столбец этой матрицы состоит из n единиц;
2. M(e) = 0n - математическое ожидание вектора возмущений равно ноль-вектору;
3. åe= M(ee¢) = W, где W - положительно определенная квадратная матрица; заметим, что произведение векторов e‘e дает скаляр, а произведение векторов ee¢ дает матрицу размерностью nxn.
4. Ранг матрицы Х равен р+1, который меньше n; напомним, что р+1 - число объясняющих переменных в модели (вместе с фиктивной переменной), n - число наблюдений за результирующей и объясняющими переменными.
Следствие 1. Оценка параметров модели (6.1) обычным МНК
| b= (X’X)-1X’Y | (6.2) |
является несмещенной и состоятельной, но неэффективной (неоптимальной в смысле теоремы Гаусса-Маркова). Для получения эффективной оценки нужно использовать обобщенный метод наименьших квадратов.
Следствие 2. Для классической модели ковариационная матрица вектора оценок параметров определялась формулой:
| åb = s2(X’X)-1. | (6.3) |
Эта оценка для обобщенной модели является смещенной (следовательно, и неэффективной). В работе [1, с. 676] эта оценка названа неработоспособной и неприменимой для обобщенной ЛММР.
Следствие 3. Для обобщенной модели ковариационная матрица вектора оценок параметров определяется другой формулой (вывод см. в работе [5, с.151]):
| åb* = (X’X)-1X’WX(X’X)-1. | (6.4) |
Дата добавления: 2019-10-16; просмотров: 575;
