Расчет на прочность
Плоским (прямым) поперечным изгибом балки называется изгиб, при котором все внешние нагрузки действуют в одной из главных плоскостей инерции балки, причем проекции внешних сил и реакций опор на ось балки равны нулю. В этом случае отличны от нуля только две из шести внутренних сил: внутренняя поперечная сила Qy и внутренний изгибающий момент Mz., действующий в этой же плоскости, где приложены внешние силы (рисунок 16).
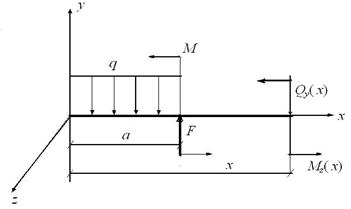
Рисунок 16 − Внутренние силы в поперечном сечении балки: Qy(х) и Mz.(х)
Эти внутренние силы определяются методом сечений из условий статического равновесия части балки, расположенной по одну сторону от рассматриваемого сечения, под действием внешней нагрузки и искомых внутренних сил, действующих со стороны отброшенной части балки. Условия статического равновесия сводятся к двум уравнениям статики: равенстве нулю суммы проекций на ось у всех сил (ΣY = 0) и равенстве нулю суммы моментов в сечении х всех сил (Σmx = 0).
Для балки ( рисунок 39) поперечная сила Qy(х) и изгибающий момент
Mz.(х) определяются из двух уравнений статического равновесия:
ΣY = F – q∙a –- Qy(х) = 0, (1)

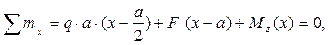 (2)
(2)
откуда
Qy(х) = F – q∙a,
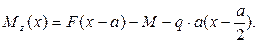
При выполнении условий (1) и (2) все остальные условия статического равновесия удовлетворяются автоматически, т. е. никаких других внутренних сил при плоском изгибе не возникнет.
Из (1) и (2) видим, что внутренняя поперечная сила Qy(х) в сечении x численно равна алгебраической сумме всех внешних сил, действующих по одну сторону от рассматриваемого сечения. Аналогично, внутренний изгибающий момент Mz(х) в сечении х численно равен алгебраической сумме моментов всех внешних нагрузок, действующих по одну сторону от рассматриваемого сечения.
Для того, чтобы внутренние силы определялись однозначно и независимо от того, равновесие какой части балки рассматривается, вводят правило знаков для Qy(х) и Mz(х).
Если внешняя сила (F, q) стремится повернуть рассматриваемую часть балки относительно центра тяжести сечения x по ходу часовой стрелки, то ее вклад во внутреннюю силу Qy(х) положителен, если против хода часовой стрелки – отрицателен (рисунок 17).
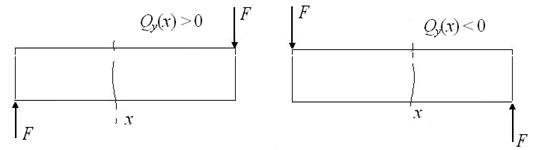
Рисунок 17 − Определение знака поперечной силы Qy(х)
Если внешняя сила (F, q, M) стремится изогнуть часть балки относительно центра тяжести сечения х выпуклостью вниз (сжатое волокно сверху), то ее вклад во внутренний момент Mz(х) положителен; если выпуклостью вверх (сжатое волокно снизу) – отрицателен (рисунок 18).
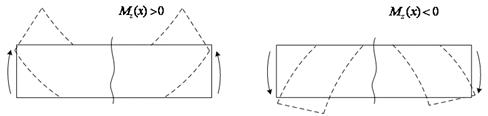
Рисунок 18 − Определение знака изгибающего момента Mz(х)
Направим ось абсцисс (ox) системы координат слева направо вдоль оси балки. Тогда внутренние усилия Qy(х), Mz(х) в поперечных сечениях и внешняя распределенная нагрузка q будут функциями x. Они связаны дифференциальными соотношениями:
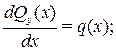 (3)
(3)
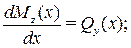 (4)
(4)
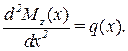 (5)
(5)
Здесь q(х) считается положительной, если она направлена вверх. Эти соотношения следует использовать при проверке правильности построения эпюр Qy(х) и Mz(х).
Внутренний изгибающий момент связан с нормальными напряжениями, которые распределяются по высоте сечения неравномерно, вызывая растяжение одной его части и сжатие другой.
Условие прочности по нормальным напряжениям для балки любой формы поперечного сечения имеет вид
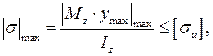 (6)
(6)
где Mz – изгибающий момент в опасном сечении балки, Н∙м;
Iz – момент инерции поперечного сечения, м4;
ymax – расстояние от нейтральной оси до наиболее удаленной точки
поперечного сечения, м.
Для балок, поперечные сечения которых симметричны относительно нейтральной оси z, условие прочности преобразуется к виду
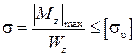 , (7)
, (7)
где Wz – осевой момент сопротивления поперечного сечения, м3.
На основании соотношений (6), (7) Wz определяется по формуле
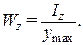
3.2.1. Построение эпюр внутренних сил Qy и Mz
Эпюрой внутренней силы называется график ее изменения вдоль оси балки. Из определения внутренней поперечной силы Qy(х) следует, что в том и только в том сечении, где приложена внешняя сосредоточенная сила, имеется скачок на эпюре Qy(х) на величину этой силы. Аналогично из определения внутреннего изгибающего момента Mz(х) следует, что в том и только в том сечении, где приложен внешний изгибающий момент, – скачок на эпюре Mz(х) на величину этого момента. Под внешними силами и моментами мы подразумеваем и реакции опор.
При проверке правильности построения эпюр Qy(х) и Mz(х) можно использовать таблицу 4, составленную на основании дифференциальных соотношений (3) – (5). В этой таблице указана связь между знаками интенсивности распределенной нагрузки q(x), поперечной силы Qy(х) и характером изменения эпюр Qy(х) и Mz(х) .
Таблица 4
Правила построения эпюр Qy(х) и Mz(х) , основанные
на дифференциальных зависимостях между q, Qy(х), Mz(х)
| Распределенная нагрузка q, кН/м | Поперечная сила Qy, кН | Изгибающий момент Mz, кН∙м |
| q=0 | Поперечная сила постоянна | Изгибающий момент изменяется по линейному закону |
| Момент постоянный | ||
| + | Момент возрастает | |
| _ | Момент убывает | |
| q >0 | Поперечная сила возрастает по линейному закону | Момент изменяется по закону параболы, выпуклость вниз |
| Момент принимает экстремальное значение Mmin | ||
| + | Момент возрастает по закону параболы, выпуклость вниз | |
| _ | Момент убывает по закону параболы, выпуклость вниз | |
| q < 0 | Поперечная сила убывает по линейному закону | Момент изменяется по закону параболы, выпуклость вверх |
| Момент принимает экстремальное значение Mmax | ||
| + | Момент возрастает по закону параболы, выпуклость вверх 
| |
| _ | Момент убывает по закону параболы, выпуклость вверх |
Пример 4
Рассмотрим построение эпюр Qy(х) и Mz.(х) методом записи и исследования их уравнений на примере расчета на прочность двухопорной балки.
Необходимо построить эпюры поперечных сил Qy и изгибающих моментов Mz для двухопорной двутавровой балки (рисунок 19) и подобрать размеры поперечного сечения при 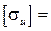 200 МПа.
200 МПа.
1. Определение опорных реакций:
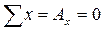 ;
;
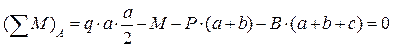 ;
;
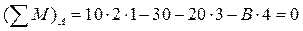 ,
, 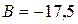 кН;
кН;
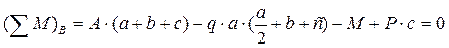 ;
;
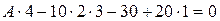 ,
, 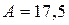 кН.
кН.
Проверка 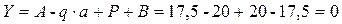
следовательно, реакции найдены верно.
2. Построение эпюр Qy и Mz.
Балка имеет три участка нагружения.
Участок I
В пределах первого участка произвольно намечаем сечение 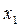
(рисунок 19): 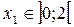 м.
м.
Для составления уравнений Qy(х1) и Mz(х1) рассмотрим условия равновесия левой (от сечения 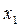 ) части балки. Поперечная сила в сечении
) части балки. Поперечная сила в сечении 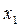 равна алгебраической сумме внешних сил по левую сторону от сечения.
равна алгебраической сумме внешних сил по левую сторону от сечения.
Учитывая правило знаков (рисунок 17), получим Qy(х) = A – q∙x1 = = 17,5 – 10∙x1 (кН) – линейная зависимость.
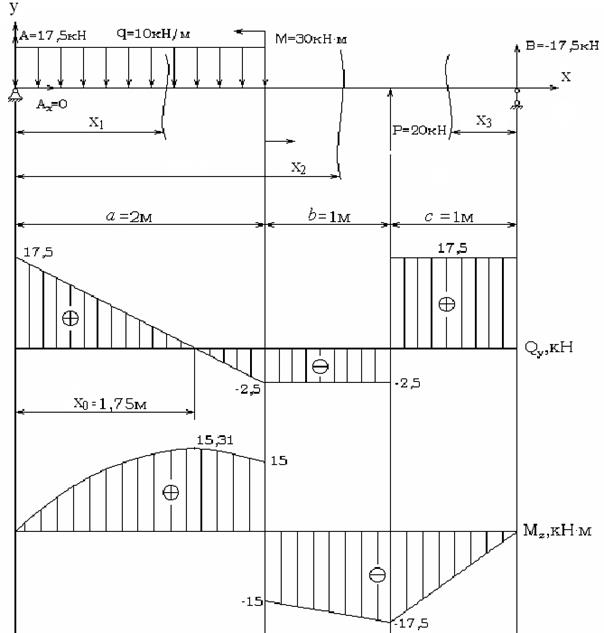
Рисунок 19 − Построение эпюр Qy(x) и Mz(x) для двухопорной балки
График поперечной силы Qy(х) можно построить по двум точкам, абсциссы которых соответствуют границам участка I:
Qy(0) = 17,5 кН; Qy(2) = – 2,5 кН.
Далее нам нужно найти точку пересечения эпюры с базисной линией, то есть 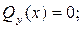
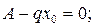
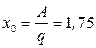 . (8)
. (8)
Внутренний изгибающий момент 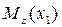 в сечении
в сечении 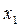 равен алгебраической сумме моментов от всех внешних нагрузок по левую сторону от сечения. С
равен алгебраической сумме моментов от всех внешних нагрузок по левую сторону от сечения. С  учетом правила знаков (рисунок 18) получим
учетом правила знаков (рисунок 18) получим
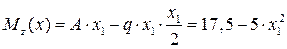 – парабола ветвями вниз. Значения на границах участка
– парабола ветвями вниз. Значения на границах участка 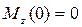 ,
, 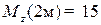 кН∙м.
кН∙м. 
Вершина параболы находится из условия
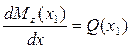 ,
,
т. е. из (8) при 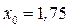 м
м 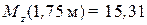 кН∙м.
кН∙м.
По трем точкам строим эпюру Mz на участке I.
Участок II
Наметив сечение 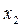 , рассмотрим левую часть балки:
, рассмотрим левую часть балки:
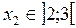 м,
м,
Qy( x2) = A – q∙2 = 17,5 –20 = – 2,5 кН – (9)
– горизонтальная прямая, тaк как Qy( x2) = – 2,5 кН – const.
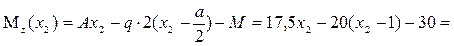 (10)
(10)
= – 2,5∙х2 – 10 кН∙м – прямая линия. 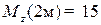 кН∙м,
кН∙м, 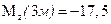 кН∙м.
кН∙м.
Можно убедиться, что из условия равновесия правой части балки
получаются те же самые выражения (9) и (10) для внутренних сил:
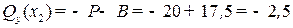 кН;
кН;
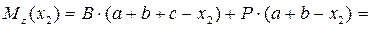
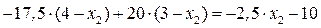 кН∙м.
кН∙м.
Участок III
Здесь проще рассматривать условие равновесия правой части балки
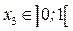 м.
м.
Учитывая правила знаков для правой части балки (рисунки 17, 18), получим: 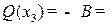 +17,5 кН – горизонтальная прямая.
+17,5 кН – горизонтальная прямая.
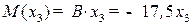 ,
,
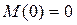 ,
, 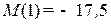 кН∙м.
кН∙м.
Построив эпюры 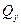 и
и 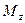 (рисунок 19), проверяем, удовлетворяют ли
(рисунок 19), проверяем, удовлетворяют ли
они правилам, сформулированным в таблице 4.
3. Расчет на прочность.
Условие прочности при прямом изгибе можно записать в виде неравенства
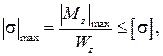
откуда находим момент сопротивления поперечного сечения.
Вычисления производим в системе СИ:
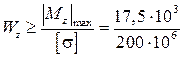 = 8,75∙10-5 м3 =87,5 см3.
= 8,75∙10-5 м3 =87,5 см3.
По сортаменту (приложение 4) определим, что такому условию
соответствует двутавр № 16, Wz = 109 см3.
3.2.2. Построение эпюр внутренних сил Qy и Mz
Дата добавления: 2019-07-26; просмотров: 506;
