Дифференциальных уравнений

С известной степенью приближения технологическая система может быть линеаризована, если в ней нет существенных нелинейностей, напри-мер зазоров, проскальзываний и др.

При оценке динамических свойств системы в качестве входной величи-ны может рассматривать подачу режущего инструмента.

Для осуществления обработки вала на токарном станке подачу режуще-го инструмента и одну из возможных выходных величин можно отсчиты-вать от одной базы, например от станины станка (рис. 20).

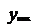
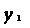
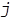
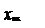
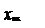
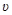
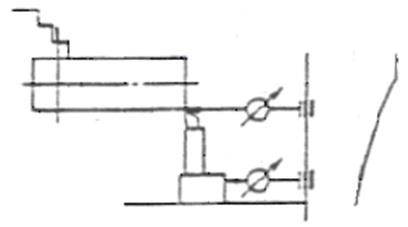
Рис. 20. Механическая модель обработки резанием

на токарном станке

Перемещение суппорта x_вх и перемещение вершины резца y_выхотлича-ется на величину прогиба резца y₁ под влиянием силы резания, т.е.

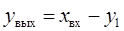. (1)

При этом сила резания F равна

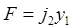, (2)

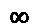где j₂ – жесткость резца. Предполагается, что жесткость детали j = .

Сила резания возникает в процессе работы привода подачи станка. Можно записать

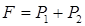, (3)

где Р₁ – сила, связанная со скоростью подачи; Р₂ – сила, пропорциональная ускорению.

Здесь ,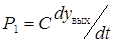

где С – коэффициент пропорциональности

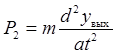, (4)

где m – масса суппорта.

С учетом выражений (1) и (2) имеем

.

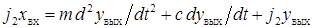Обозначим 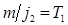; 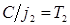. Получим

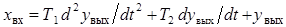. (5)

Записанное уравнение (5) представляет собой дифференциальное урав-нение, которое указывает на то, что технологическая система может рас-сматриваться как звено второго порядка.

Качество уравнения зависит от быстродействия системы, продолжи-тельности переходных процессов, зависящей от 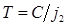, запаса устойчи-вости. Появление в работе скачкообразных перемещений узлов, вибраций заготовки и(или) инструмента и другого свидетельствует о потери устой-чивости.

Математическое описание динамики САУ осуществляется путем сос-тавления системы дифференциальных уравнений. Строго говоря, любая реальная динамическая система является нелинейной. Однако в большин-стве случаев описание непрерывных процессов может быть заменено приб-лиженно эквивалентными процессами, которые описывают обыкновенны-ми линейными дифференциальными уравнениями. Такую систему принято называть линеаризованной (рис. 21).

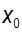
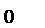
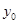
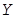
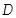
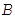
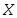
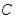
Рис. 21. Графическая интерпретация

процедуры линеаризации