Глава 3. Решения систем линейных алгебраических уравнений

В вычислительной математике используется два класса численных методов решения систем линейных алгебраических уравнений (СЛАУ):

1. Прямые (или точные) методы, позволяющие найти решение за определенное количество шагов. К ним относятся метод Гаусса, метод Крамера, метод Халецкого и другие.

2. Итерационные методы, основанные на использовании повторяющегося процесса и позволяющие получить решение в результате последовательных приближений. К ним относятся метод итераций, метод Зейделя, метод релаксаций и другие.

Метод итераций

Дана система, состоящая из n линейных уравнений с n неизвестными:

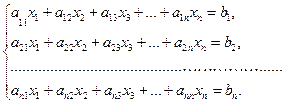(3.1)

Обозначим через 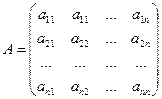-матрицу коэффициентов системы (3.1), через 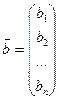- столбец свободных членов и через 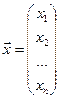- столбец неизвестных.

Тогда систему (3.1) можно записать в виде матричного уравнения

.

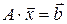Решением системы будут числа x₁, x₂, …, x_n. Определитель системы не равен нулю. Предполагая, что диагональные коэффициенты 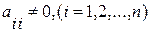разрешим первое уравнение системы относительно x₁, второе – относительно x₂ и т.д. Тогда получим равносильную систему, которая называется приведенной к виду , удобному для итераций.

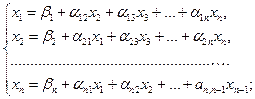, (3.2)

где 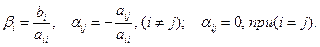(3.3)

Введем в рассмотрение матрицы:

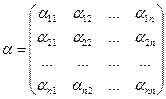и .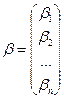

Тогда систему можем записать в матричном виде:

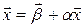. (3.2')

Заметим, что систему (3.1) можно приводить к виду (3.2) любыми линейными преобразованиями. Систему (3.2) будем решать методом последовательных приближений, используя матричную запись. За нулевое приближение принимаем, например, столбец свободных членов: 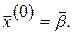Далее последовательно строим матрицы-столбцы: 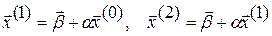и т.д.

Любое (k+1)-ое приближение вычисляют по формуле:

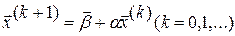. (3.4)

Если последовательность приближений 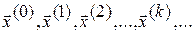имеет предел 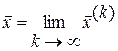, то этот предел является решением системы (3.2). В самом деле, переходя к пределу в равенстве (3.4), будем иметь: 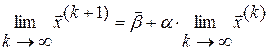или 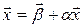т.е. предельный вектор 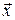является решением системы.

Напишем формулы приближений в развернутом виде:

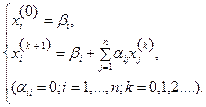
Метод итераций – метод последовательных приближений. Процесс итерации хорошо сходится, т.е. число приближений, необходимых для получения корней системы с заданной точностью, невелико, если элементы матрицы a малы по абсолютной величине. Иными словами, для успешного применения процесса итерации модули диагональных коэффициентов системы должны быть велики по отношению к модулям недиагональных коэффициентов этой системы. Свободные члены при этом роли не играют.

Выясним, при каких достаточных условиях последовательность приближений 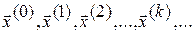имеет предел.

Теорема 3.1

Если для приведенной системы выполнено, по меньшей мере, одно из условий:

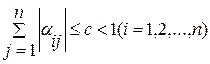или ,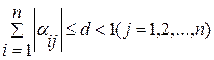

то процесс итерации сходится к единственному решению этой системы, независимо от выбора начального приближения.

В теореме (3.1) - «с» это значение максимальной суммы модулей элементов в строках, а «d» в столбцах матрицы α. Эти числа называют нормой матрицы α по строкам и по столбцам соответственно.

Следствие из теоремы (3.1).

Для приведенной системы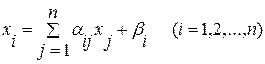

полученной из системы 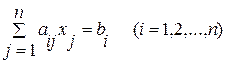по формулам (3.3)

метод итераций сходится, если выполнены неравенства

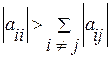(i=1,2,…n),

т.е. модули диагональных коэффициентов системы больше суммы модулей всех остальных коэффициентов.