Оценка погрешности приближений процесса итераций
Пусть 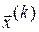 и
и 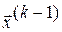 - два последовательных приближения системы (3.2). Тогда для приближения
- два последовательных приближения системы (3.2). Тогда для приближения 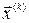 справедлива оценка
справедлива оценка
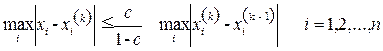 :,
:,
если выполнено первое условие теоремы 3.1, или
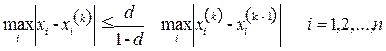 ,
,
если выполнено второе условие теоремы 3.1. Процесс итерации заканчивают, когда указанные оценки свидетельствуют о достижении заданной точности ε.
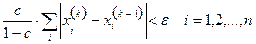
или
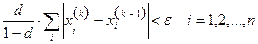
3.1.2. Приведение линейной системы к виду, удобному для итерации:
Сходимость накладывает жесткие условия на коэффициенты данной линейной системы 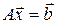 . Однако, если
. Однако, если 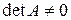 , то с помощью линейного комбинирования уравнений системы, последнюю всегда можно заменить эквивалентной системой
, то с помощью линейного комбинирования уравнений системы, последнюю всегда можно заменить эквивалентной системой 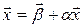 , такой, что условия сходимости будут выполнены. Умножим уравнение (3.1) на матрицу
, такой, что условия сходимости будут выполнены. Умножим уравнение (3.1) на матрицу 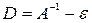 , где
, где 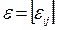 - матрица с малыми по модулю, одинаковыми элементами. Тогда будем иметь:
- матрица с малыми по модулю, одинаковыми элементами. Тогда будем иметь:
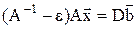
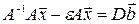
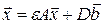
или 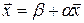 , где
, где 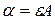 и
и 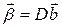 .
.
Все элементы матрицы ε выбираем одинаковыми из условия 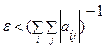 . Это обеспечивает выполнение достаточного условия сходимости метода.
. Это обеспечивает выполнение достаточного условия сходимости метода.
Пример 3.1 Решить систему методом итераций в Mathcad с тремя верными цифрами после запятой
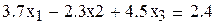
|
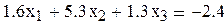
|
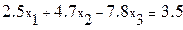
|
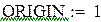
|
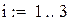
|
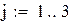
|
Точность вычислений 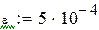
Решение исходной системы матричным методом
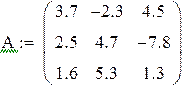
|
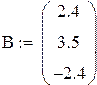
|
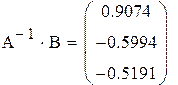
|
Линейными преобразованиями добиваемся диагонального преобладания.
| 2*I+II II+2*III II-3III |
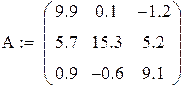
|
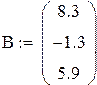
|
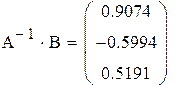
|
Преобразуем к виду, удобному для итераций.
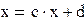
|
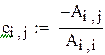
|
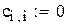
|
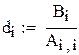
|
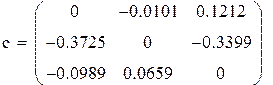
|
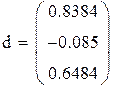
|
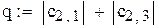
|
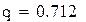
|
q-это норма матрицы «с»
В качестве начального приближения возьмем столбец свободных членов, сделаем 6 приближений, вектор разностей между соседними приближениями обозначим z. Результаты поместим в матрицу x.
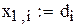
|
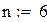
|
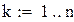
|
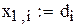
|
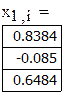
|
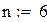
|
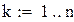
|
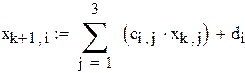
|
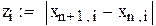
|
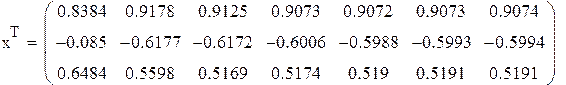
|
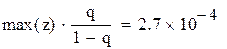
|
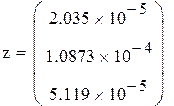
|
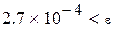
|
Ответ: 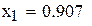
|
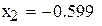
|
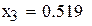
|
Рис. 3.1.Решение примера 3.1 в Mathcad
Метод Зейделя
Метод Зейделя является модификацией метода итерации. Он заключается в том, что при вычислении (k+1)-го приближения неизвестного 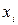 при i>1 используют уже вычисленные ранее (k+1)-е приближения неизвестных
при i>1 используют уже вычисленные ранее (k+1)-е приближения неизвестных 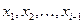
Пусть дана приведенная линейная система 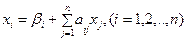
Выберем произвольно начальные приближения корней 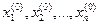 ,
,
Далее, предполагая, что k-е приближения 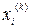 корней известны, согласно Зейделю будем строить (k+1)-е приближения корней по следующим формулам:
корней известны, согласно Зейделю будем строить (k+1)-е приближения корней по следующим формулам:
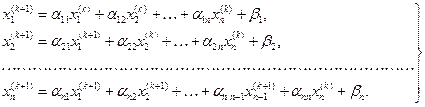
Процесс повторяется до тех пор, пока разница между двумя соседними приближениями не будет меньше необходимой точности.
Условия сходимости те же, что и для метода итераций.
Пример 3.2. Пусть дана линейная система и приближенные корни системы:
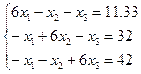 и
и 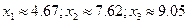 .
.
Приведем систему к виду, удобному для итераций
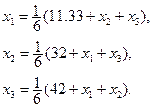
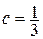 поэтому метод сходится
поэтому метод сходится
Взяв в качестве начальных приближений: 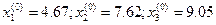 , получим:
, получим:
при k=1 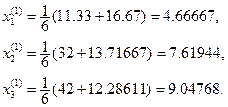
при k = 2 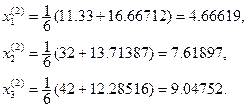
Найдем разность по модулю между соседними приближениями:
| 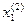 -
- 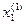 | = 0,00048
| = 0,00048
| 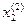 -
- 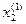 | = 0,00047
| = 0,00047
| 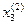 -
- 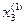 | = 0,00016
| = 0,00016
Так как для приведенной системы выполняется условие сходимости при 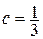 ,то полученное приближение имеет погрешность, не превышающую 0,0005.
,то полученное приближение имеет погрешность, не превышающую 0,0005.
Таким образом, в качестве решения можем принять 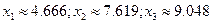 .
.
Метод релаксаций
Пусть дана система: (3.1)
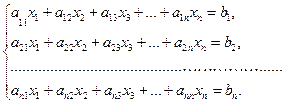
Преобразуем эту систему следующим образом: перенесем свободные члены налево и разделим первое уравнение на 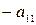 , второе – на
, второе – на 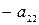 и т.д. Тогда получим систему, приготовленную к релаксации:
и т.д. Тогда получим систему, приготовленную к релаксации: 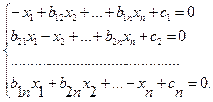 , где
, где 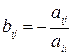
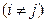 и
и 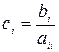 .
.
Пусть 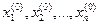 - начальное приближение решения системы. Подставляя эти значения в систему, получим в правых частях уравнений системы некоторые числовые значения . Будем называть их невязками. Невязки обращаются в нуль при подстановке корней в уравнения системы
- начальное приближение решения системы. Подставляя эти значения в систему, получим в правых частях уравнений системы некоторые числовые значения . Будем называть их невязками. Невязки обращаются в нуль при подстановке корней в уравнения системы
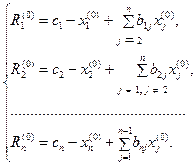 .
.
Если одной из неизвестных 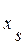 дать приращение
дать приращение 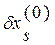 , то соответствующая невязка
, то соответствующая невязка 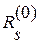 уменьшится на величину
уменьшится на величину 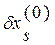 , а все остальные невязки
, а все остальные невязки 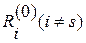 увеличатся на величину
увеличатся на величину 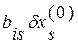 . Таким образом, чтобы обратить очередную невязку
. Таким образом, чтобы обратить очередную невязку 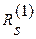 в нуль, достаточно величине
в нуль, достаточно величине 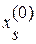 дать приращение
дать приращение 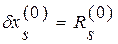 и мы будем иметь
и мы будем иметь 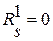 и
и 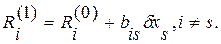
Суть метода заключается в том, чтобы на каждом шаге обращать в нуль максимальную по модулю невязку, изменяя значения соответствующей компоненты приближения. Процесс заканчивается, когда все невязки преобразованной системы будут равны нулю с заданной степенью точности.
Пример3.1: Пусть дана линейная система. Решить с точностью 0.01.
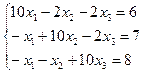 .
.
Приведем систему к виду, удобному для релаксации:
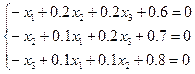 .
.
Выбирая в качестве начальных приближений корней нулевые значения 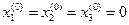 , находим
, находим 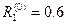 ,
, 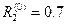 ,
, 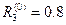 .
.
Согласно общей теории полагаем: 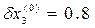 . Отсюда получаем невязки
. Отсюда получаем невязки
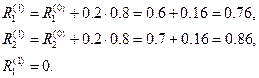
Далее полагаем 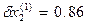
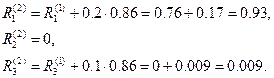
Суммируя все приращения 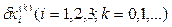 получим значения корней:
получим значения корней:
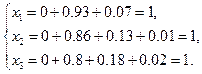
Удобно располагать вычисления в таблице:
| x1 | R1 | x2 | R2 | x3 | R3 |
| 0.93 | .60 0.16 | 0.86 | 0.70 0.16 | 0,80 0.18 | 0.80 -0.80 |
| 0.76 0.17 | 0.86 -0.86 | 0.09 | |||
| 0.93 -0.93 | 0.13 | 0.09 | 0.09 0.09 | ||
| 0.07 | 0.04 | 0.09 0.04 | 0.18 -0.18 | ||
| 0.04 0.03 | 0.13 -0.13 | 0.02 | 0.01 | ||
| 0.07 -0.07 | 0.01 | 0.01 | 0.01 0.01 | ||
| 0.01 | 0.02 -0.02 | ||||
| 0.01 -0.01 | |||||
| 1.00 | 1.00 | 1.00 |
Ответ: 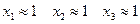
Дата добавления: 2017-05-18; просмотров: 1780;
