Модифицированный метод Ньютона
Если производная 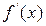 мало изменяется на отрезке [a,b] то в формуле
мало изменяется на отрезке [a,b] то в формуле 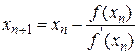 можно положить
можно положить 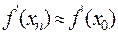 . Отсюда для корня
. Отсюда для корня 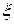 уравнения
уравнения 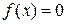 получаем последовательные приближения по формуле
получаем последовательные приближения по формуле 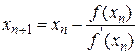 (n=0,1,…)..
(n=0,1,…)..
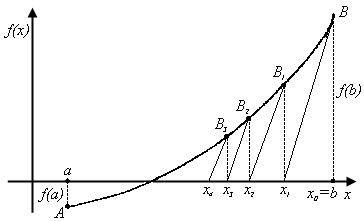
Рис.2.9. Модифицированный метод Ньютона
Оценка точности делается, как в методе Ньютона.
Метод секущих
Заменим производную функции f(x) в точке xn на функцию F(x) в этой же точке. Подставим ее вместо производной в формулу Ньютона.
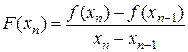 ,
,
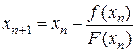 .
.
В методе секущих требуются задать для начала счета два значения x0 и x1. Отрезок [x0, x1] не обязательно должен содержать корень уравнения.
Оценка точности делается, как в обыкновенном методе Ньютона
Метод итераций
Пусть дано уравнение
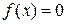 , (2.1)
, (2.1)
где 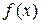 - непрерывная функция. Заменим его равносильным уравнением
- непрерывная функция. Заменим его равносильным уравнением
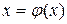 . (2.2)
. (2.2)
Выберем каким-либо способом приближенное значение корня 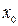 и подставим его в правую часть уравнения (2). Получим некоторое число
и подставим его в правую часть уравнения (2). Получим некоторое число 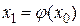 . Повторим данную процедуру с x1, получим
. Повторим данную процедуру с x1, получим 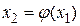 . Повторяя описанную процедуру, будем иметь последовательность чисел:
. Повторяя описанную процедуру, будем иметь последовательность чисел:
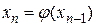 , где n=1,2,…. (2.3)
, где n=1,2,…. (2.3)
Пусть у этой последовательности существует предел 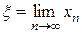 . Перейдем к пределу в равенстве (2.3). Предполагая функцию φ(х) непрерывной, найдем:
. Перейдем к пределу в равенстве (2.3). Предполагая функцию φ(х) непрерывной, найдем: 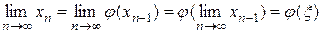 или
или 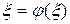 .
.
Таким образом, предел является корнем уравнения 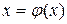 и может быть вычислен по формуле (2.3) с любой степенью точности.
и может быть вычислен по формуле (2.3) с любой степенью точности.
На рисунке дана геометрическая интерпретация метода итераций в зависимости от знака производной функции φ(х).
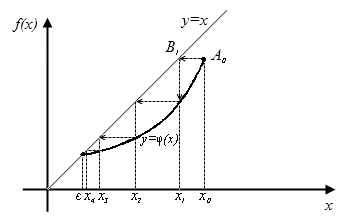
Рис 2.10 φ'(х) > 0.
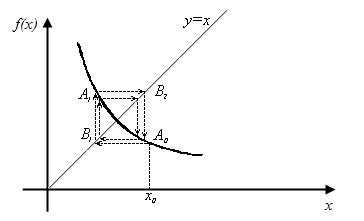
Рис.2.11 φ'(х) < 0
Достаточное условие сходимости процесса итераций определяется в следующей теореме.
Теорема 2.3: Пусть функция 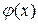 определена и дифференцируема на отрезке
определена и дифференцируема на отрезке 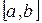 , причем все ее значения
, причем все ее значения 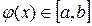 . Тогда, если существует правильная дробь q такая, что
. Тогда, если существует правильная дробь q такая, что 
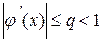 при
при 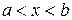 , то
, то
1. процесс итерации 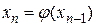 (n=1,2,..) сходится независимо от начального значения
(n=1,2,..) сходится независимо от начального значения 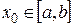 ;
;
2. предельное значение 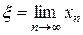 является единственным корнем уравнения
является единственным корнем уравнения 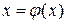 на отрезке
на отрезке 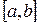 при
при 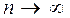 .
.
Для оценки погрешности приближения xn получается формула:
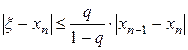 ,
,
где 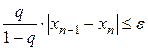 ; а
; а 
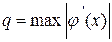 на [a,b] При заданной точности ответа ε итерационный процесс прекращается, если
на [a,b] При заданной точности ответа ε итерационный процесс прекращается, если
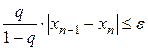 . Если q<|0.5|
. Если q<|0.5|  , то
, то 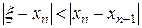 .
.
Сходимость итерационной последовательности определяется видом функции φ(х). Преобразование к виду (2.2) можно провести различными способами. Чтобы обеспечить сходимость, можно искать решение в виде
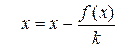 , (2.4)
, (2.4)
где k-целое число. Уравнение (2.4) это уравнение (2.1) с 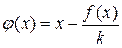 . Оно равносильно исходному уравнению (2.1). Для сходимости метода итераций по теореме 2.3 необходимо, чтобы
. Оно равносильно исходному уравнению (2.1). Для сходимости метода итераций по теореме 2.3 необходимо, чтобы 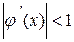 . Дифференцируем φ(х) и получаем
. Дифференцируем φ(х) и получаем 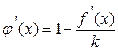 . Решаем неравенство
. Решаем неравенство 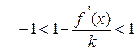 :
:
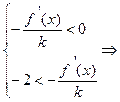
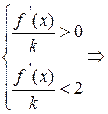
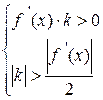 .
.
Чтобы условие сходимости выполнялось на всем промежутке [a,b], нужно взять 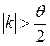 , где
, где 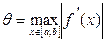 .
.
Итак, если выполняются условия 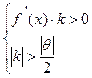 то метод итераций сходится для уравнения
то метод итераций сходится для уравнения 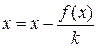
Пример 2.6. Методом итераций найти корень уравнения
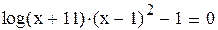
на промежутке (-10,-9,6) с четырьмя знаками после запятой.
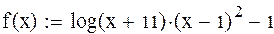
| Находим производную f(x) |
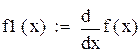
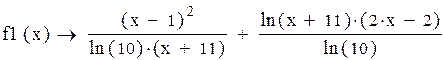
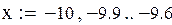

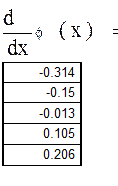
По значению производной f(x) выбираем положительное k
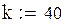
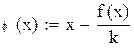
В качестве начального приближения выберем левый конец промежутка. Сделаем шесть итераций.
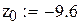
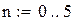
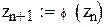
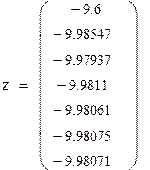
Так как значения производной φ(x) по модулю меньше 0.5, то оцениваем точность вычислений по формуле 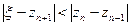

|
Корень уравнения x = -9.98071 найден с точностью 0.000038
Рис. 2.12. Вычисления в Mathcad, реализующие метод итераций для примера 2.6
Дата добавления: 2017-05-18; просмотров: 2053;
