Метод половинного деления
Пусть уравнение (2.1) имеет на отрезке [a,b] один корень, а функция f(x) на данном отрезке непрерывна и f(a)·f(b)<0. Разделим отрезок [a,b] пополам точкой x1=(а+b)/2. Если f(x1)≠0 , то для продолжения вычислений выберем ту часть промежутка, где знаки функции различны. Концы полученного отрезка обозначим [a1,b1] и снова разделим отрезок [a1,b1] пополам точкой x2=( a1+ b1)/2 и т. д. В результате на каком-то этапе получим или точный корень уравнения(2.1) или бесконечную последовательность вложенных друг в друга отрезков [a1,b1], [a2,b2],… [an,bn],…таких, что
f(an)·f(bn)<0, (n=1,2,…) (2.2)
bn - an=2 -n·(b-a). (2.3)
Так как левые концы a1, a2,… ,an образуют монотонную неубывающую ограниченную последовательность, а правые концы b1 b2,…,bn образуют монотонную невозрастающую ограниченную последовательность, а расстояние между ними в силу (2.2) стремится к нулю, то у последовательностей существует общий предел . Число ξ, которое является общим пределом последовательностей {an} и {bn}, точный корень уравнения (2.1). Оценим погрешность решения на n-м шаге. Считаем до тех пор, пока длина промежутка не станет меньше заданной точности ε.
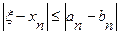
В качестве ответа возьмем середину отрезка [an,bn].
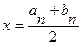 .
.
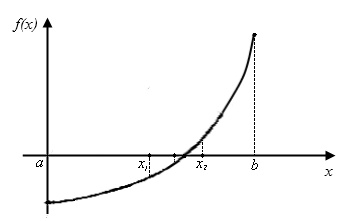
Рис.2.2. К объяснению метода половинного деления
Метод половинного деления практически удобно применять для грубого нахождения корня данного уравнения, так как при увеличении точности значительно возрастает объём вычислений.
Пример 2.3. Найти, используя пакет Matchcad, методом половинного деления корень уравнения x4-x3-2x2+3x-3=0 на промежутке [1,2]
Функция koren(a,b,ε) возвращает длину отрезка, который будет меньше заданной точности ε, и значение корня на этом промежутке, если на концах отрезка [a,b] функция имеет противоположные знаки, или сообщение об отсутствии корня, в противном случае.
Метод легко реализуется на компьютере. Далее приводится листинг программы, написанной на языке, встроенном в систему Mathcad.
 Рис. 2.3. Листинг программы в Mathcad, реализующей метод половинного деления для примера 2.3
Рис. 2.3. Листинг программы в Mathcad, реализующей метод половинного деления для примера 2.3
Метод хорд
В этом методе нелинейная функция f(x) на отделенном промежутке
[a,b] заменяется хордой, проходящей через точки (a,f(a))и (b,f(b))
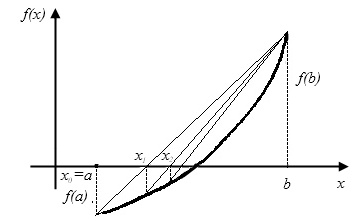
Рис.2.4. Метод хорд. Неподвижен правый конец промежутка b
Уравнение хорды: 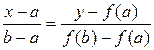 . Найдем точку пересечения хорды с горизонтальной осью. Полагая
. Найдем точку пересечения хорды с горизонтальной осью. Полагая 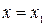 и
и 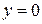 , получим
, получим
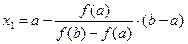 .
.
Точку x1 принимаем за новую границу отрезка, где содержится корень. Через эту точку с координатами (x1,f(x1)) и соответствующую границу предыдущего интервала (b,f(b)) опять проводим хорду, находим 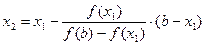 и т.д., получая последовательность x1,x2,x3,…xn,…, сходящуюся к корню уравнения.
и т.д., получая последовательность x1,x2,x3,…xn,…, сходящуюся к корню уравнения.
Вторая производная 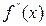 сохраняет постоянный знак на
сохраняет постоянный знак на 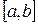 . Следовательно, возможны два случая. Если f(b)·f "(b)>0, то хорда имеет правый фиксированный конец, причем последовательность x0,x1,…xn приближается к корню слева. За начальное приближение x0, естественно, берут a
. Следовательно, возможны два случая. Если f(b)·f "(b)>0, то хорда имеет правый фиксированный конец, причем последовательность x0,x1,…xn приближается к корню слева. За начальное приближение x0, естественно, берут a
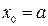 ;
; 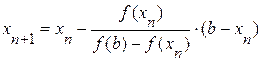 ;
; 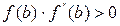 ;
;
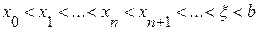 .
.
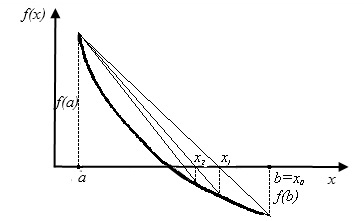
Рис.2.5. Метод хорд. Неподвижен левый конец промежутка a
Если f(a)·f "(a)>0, то хорда имеет левый фиксированный конец, причем последовательность x0,x1,…xn … приближается к корню справа. За начальное приближение x0, берут b
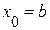 ;
; 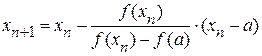 ;
; 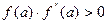 ;
;
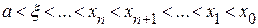 .
.
Для оценки точности можно воспользоваться формулой
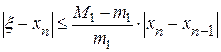 ,
,
где 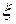 -точный корень,
-точный корень, 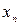 - приближенный корень,
- приближенный корень, 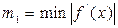 ,
, 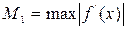 на промежутке [a,b]. Считаем до тех пор пока, не выполнится условие
на промежутке [a,b]. Считаем до тех пор пока, не выполнится условие 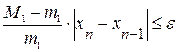 . Если имеет место неравенство
. Если имеет место неравенство 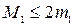 , то счет можно прекратить, когда.
, то счет можно прекратить, когда. 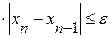
Пример 2.4. Найти методом хорд корень уравнения x4-x-1=0
Решение находим, используя пакет Mathcad.
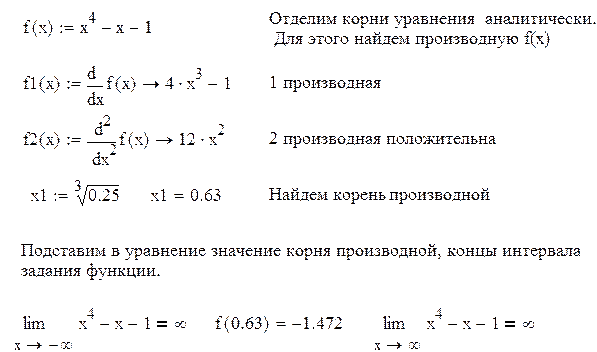
Функция монотонна на промежутках (-∞, 0.63), (0.63, ∞) и меняет на концах промежутков знак. Уравнение имеет два корня. Сузим промежутки отделения корней методом проб, т.е. подстановкой.
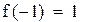
|
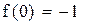
|
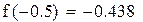
|
Первый корень принадлежит промежутку (-1,-0.5)
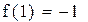
|
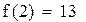
|
Второй корень принадлежит промежутку (1,1.5)
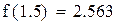
|
Будем находить корень на промежутке (-1,-0.5)
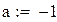
|
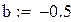
|
Вторая производная всюду положительна, функция положительна в точке a = -1, значит, этот конец неподвижен.
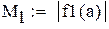
|
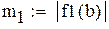
|
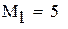
|
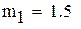
|
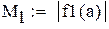
|
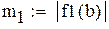
|
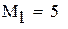
|
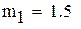
|
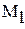 -максимальное, a -максимальное, a 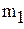 -минимальное значение модуля производной
на промежутке -минимальное значение модуля производной
на промежутке
|
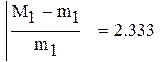
|
так как 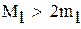 , множитель
, множитель 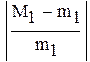
нужно учитывать при оценке точности решения,
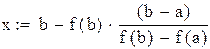
|
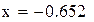
|
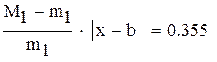
|
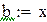
|
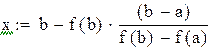
|
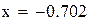
|
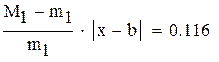
|
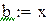
|
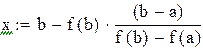
|
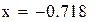
|
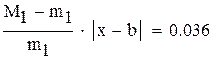
|
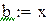
|
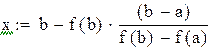
|
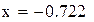
|
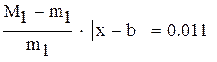
|
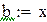
|
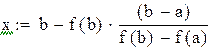
|
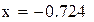
|
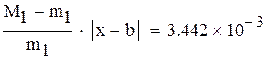
|
Нашли корень исходного уравнения 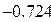 с точностью
с точностью 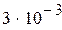 .
.
Рис. 2.6. Вычисления в Mathcad, реализующие метод хорд для примера 2.4
2.2.3. Метод Ньютона – метод касательных
Пусть 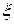 - корень уравнения
- корень уравнения 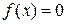 отделен на отрезке
отделен на отрезке 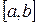 , причем
, причем 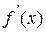 и
и 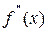 непрерывны и сохраняют определенные знаки на этом же отрезке
непрерывны и сохраняют определенные знаки на этом же отрезке 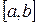 . Найдя какое-нибудь n-е значение корня
. Найдя какое-нибудь n-е значение корня 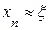 (
( 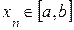 ), уточним его по методу Ньютона. Для этого положим
), уточним его по методу Ньютона. Для этого положим 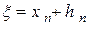 , где
, где 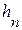 - считаем малой величиной. Разложим функцию f(x) в ряд Тейлора в окрестности точки x n по степеням h n . Тогда можно записать:
- считаем малой величиной. Разложим функцию f(x) в ряд Тейлора в окрестности точки x n по степеням h n . Тогда можно записать:
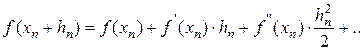
Ограничимся двумя членами ряда и так как 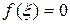 , то:
, то:
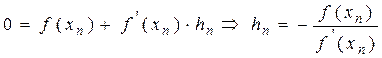 .
.
Учитывая найденную поправку hn:,получим 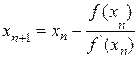 (n=0,1,2,…).
(n=0,1,2,…).
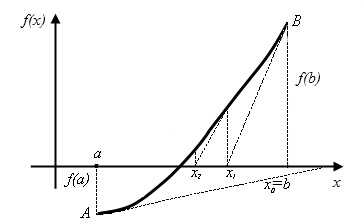
Рис.2.7 Метод касательных. Начальное приближение x0=b
По-другому этот метод называется методом касательных. Если в точке 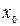 провести касательную к функции f(x) , то ее пересечение с осью ОХ и будет новым приближением x1 корня уравнения
провести касательную к функции f(x) , то ее пересечение с осью ОХ и будет новым приближением x1 корня уравнения
Хорошим начальным приближением 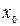 является то значение, для которого выполнено неравенство
является то значение, для которого выполнено неравенство 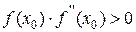 . Погрешность вычислений
. Погрешность вычислений 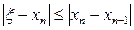 Счет можно прекратить, когда
Счет можно прекратить, когда 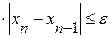
Теорема 2.2: Если 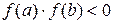 , причем
, причем 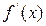 и
и 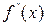 отличны от нуля и сохраняют определенные знаки при
отличны от нуля и сохраняют определенные знаки при 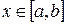 , то, исходя из начального приближения
, то, исходя из начального приближения 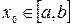 , удовлетворяющего условию
, удовлетворяющего условию 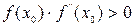 , можно вычислить методом Ньютона единственный корень
, можно вычислить методом Ньютона единственный корень 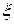 уравнения
уравнения 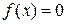 с любой степенью точности.
с любой степенью точности.
Пример 2.5. Найти методом Ньютона корень уравнения x4-x-1=0,
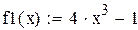
|
| 1-я производная |
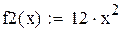
|
| 2-я производная положительна |
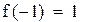
|
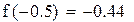
|
| один корень лежит на промежутке (-1.-0.5), второй на промежутке (1.1.5) Уточним левый корень методом Ньютона |
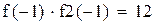
|
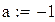
|
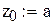
|
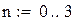
|
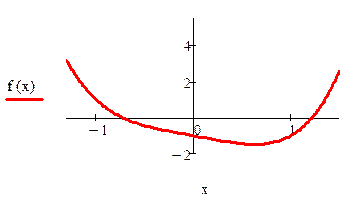
|
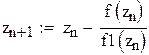
|

|
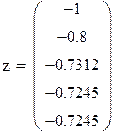
|
Нашли корень исходного уравнения -0.7245 с точность 0.00007.
Рис. 2.8. Вычисления в Mathcad, реализующие метод касательных для примера 2.5
Дата добавления: 2017-05-18; просмотров: 3651;
