Критерий Рауса-Гурвица

Это алгебраический критерий, основанный на использовании коэффициентов характеристического уравнения (13-2). Нужно составить квадратную матрицу, также она называется матрицей Гурвица, это квадратная матрица n×n. Матрица имеет вид:

.

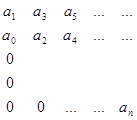Матрица состоит из коэффициентов характеристического уравнения, свободные места в матрице заполняются нулями. Далее последовательно вычисляются диагональные миноры, все диагональные миноры должны быть положительными, чтобы система была устойчива.

Если хотя бы один минор отрицателен, то система неустойчива.

Если коэффициенты характеристического уравнения знакопеременны, то система обязательно неустойчива, и матрицу можно не составлять.

Критерий Михайлова

Критерий Михайлова так же работает на основании характеристического уравнения и получаемого на его основе характеристического вектора или вектора Михайлова.

Система устойчива, если при изменении частоты от нуля до бесконечности годограф характеристического вектора, начинаясь на вещественной положительной полуоси проходит последовательно против часовой стрелки n квадрантов комплексной плоскости (где n – порядок характеристического уравнения, он же порядок системы). Говоря иначе, характеристический вектор должен совершать поворот против часовой стрелки на угол n*90.

Для получения характеристического вектора в характеристическом уравнении нужно заменить s на jω. Формула для характеристического вектора приводится ниже:

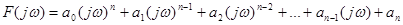. (13-3)

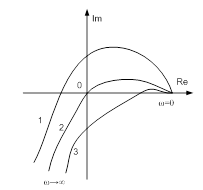
Если годограф проходит через начало координат, то система находится на границе устойчивости. Если годограф проходит не через то количество квадрантов или не в том порядке, то система неустойчива. Годографы для устойчивой системы, неустойчивой системы и системы на границе устойчивости показаны на рис. 13-2.

Рис. 13-2. Примеры годографов характеристического вектора для различных систем.

Годограф 1 соответствует устойчивой системе, годограф 2 соответствует системе на границе устойчивости, годограф 3 - неустойчивой системе.

Критерий Найквиста

Критерий Найквиста применяется для АСР с обратной связью и позволяет судить о поведении замкнутой АСР по поведению разомкнутой. Он формулируется следующим образом.

Если разомкнутый контур устойчив и годограф КЧХ разомкнутой АСР не охватывает точку на комплексной плоскости с координатами -1, j0, то после замыкания система сохранит устойчивость.

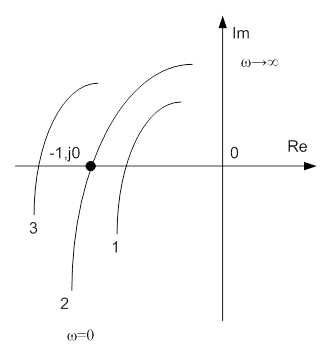
Если годограф проходит через эту точку, система находится на границе устойчивости. Если годограф охватывает эту точку, система неустойчива. Примеры годографов приведены на рис. 13-3.

Рис. 13-3. Примеры годографов КЧХ разомкнутой АСР.

Запас устойчивости