Оценка запаса устойчивости систем управления по частотным характеристикам

Запас устойчивости системы можно оценить не только по расположению корней характеристического уравнения, но и по импульсной переходной характеристике замкнутого контура системы, это достаточно наглядный способ. При этом степень затухания СТРОГО определена только для систем второго порядка, Поэтому проще перейти к изображениям по Фурье.

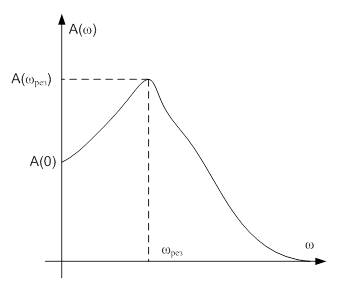
Если на АЧХ системы имеется пик, то переходный процесс имеет колебательный характер (переходная характеристика системы, импульсная переходная характеристика системы и т.д.), это справедливо для систем любого порядка, в том числе и с запаздыванием. Пик на АЧХ называется резонансным пиком.

Высота резонансного пика зависит от приближения КЧХ разомкнутой системы к точке -1,j0, при этом чем ближе КЧХ к этой точке, тем выше пик. Если КЧХ проходит через эту точку, то система находится на границе устойчивости и пик на АЧХ будет бесконечно большим (рис. 15-1).

Рис. 15-1. Оценка запаса устойчивости по пику на АЧХ.

Для численной оценки запаса устойчивости вводится величина под названием частотный показатель колебательности:

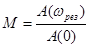. (15-1)

Если в состав алгоритма регулирования входит И-звено, то значение АЧХ при нулевой частоте равно единице, в иных случаях (например, для систем с П-регулятором) значение отлично от единице, но обычно близко к ней.

М можно принять в качестве меры запаса устойчивости, можно считать, что контур обладает необходимым запасом устойчивости, если M≤M_доп.

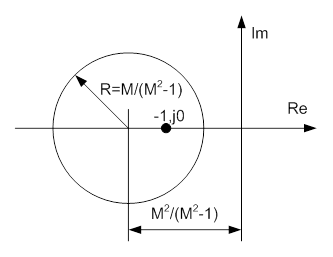
Геометрически на комплексной плоскости, оказывается, можно начертить окружность, с помощью которой можно оценить запас устойчивости. Данная окружность называется М-окружность, ее центр лежит на вещественной отрицательно полуоси, положение центра этой окружности и ее радиус зависят от М (рис. 15-2).

Рис. 15-2. М-окружность.

Необходимо отметить, что точка -1,j0 всегда будет внутри М-окружности, при этом она никогда не совпадет с её центром.

При различных значениях М получается семейство неконцентрических окружностей, при этом чем больше М, тем меньше окружность.

Таким образом, можно сформулировать, что замкнутый контур удовлетворяет требуемому запасу устойчивости, если КЧХ разомкнутого контура не заходит внутрь области, ограниченной М-окружностью (то есть, внутрь М-окружности). Предельно допустимые значения параметров системы получаются при касании окружности годографа КЧХ разомкнутой системы.