Понятие запаса устойчивости. Оценка запаса устойчивости по расположению корней характеристического уравнения

Реальные динамические системы должны быть не просто устойчивы, но и обладать определенным запасом устойчивости, то есть, возникающие в них переходные процессы должны не просто затухать, но и затухать достаточно интенсивно.

Переходные процессы в динамических системах представляют собой сумму компонентов, для вещественных корней –α_i компонент имеет вид 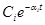, для комплексно-сопряженных корней

–α+jω компонент имеет вид 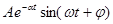. Комплексно-сопряженным корням соответствуют колебательные компоненты.

Интенсивность затухания колебательной составляющей оценивается по уменьшению амплитуд, направленных в одну сторону, величина, характеризующая это, называется степенью затухания и вычисляется по формуле:

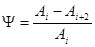. (14-2)

Для систем второго порядка так же можно записать

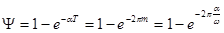. (14-3)

Величина 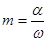называется корневым показателем колебательности. Чем меньше корневой показатель колебательности, тем хуже затухание колебаний.

Критерий Дудникова (Обобщенный критерий Найквиста)

Критерий Найквиста позволяет судить только об устойчивости системы, но не о запасе устойчивости. Чтобы судить о запасе устойчивости системы, этот критерий необходимо модифицировать, таким образом получается критерий Дудникова, он же обобщенный критерий Найквиста. Формулируется он следующим образом.

Если все комплексные компоненты характеристического уравнения разомкнутого контура системы имеют корневой показатель колебательности не меньше заданного, то после замыкания контура все компоненты переходного процесса будут также иметь значение этого показателя не ниже заданного, если так называемая расширенная частотная характеристика разомкнутого контура не охватывает точку -1,j0 на комплексной плоскости.

Расширенная КЧХ получается из обычной КЧХ следующим образом: .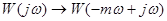

Соответственно, система имеет запас устойчивости не хуже заданного, если все корни характеристического уравнения системы удовлетворяют условию 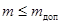. Геометрический смысл этого утверждения показан на рис. 14-3.

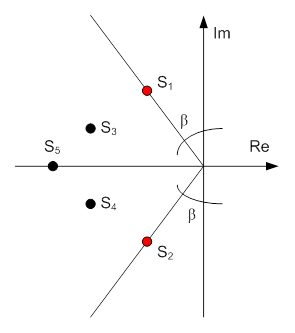
Рис. 14-3. Геометрический смысл запаса устойчивости по расположению корней характеристического уравнения.

Можно записать, что 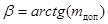, корни лежащие на лучах, расходящихся под этими углами к оси к мнимой оси (то есть, корни S₁ и S₂), называются доминирующими. Все прочие корни должны лежать внутри угла, образованного этими лучами.

Причиной возможной неустойчивости системы может быть наличие контуров, поэтому при расчетах на устойчивость необходимо пользоваться характеристиками замкнутых контуров, а не характеристиками возмущений.