Расчет оптимальный параметров настройки ПИ-регулятора при ограничении на корневой показатель колебательности

Запишем уравнение границы устойчивости в соответствии с критерием Найквиста:

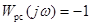. (17-1)

Запишем уравнение границы области заданного запаса устойчивости в соответствии с критерием Дудникова:

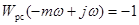. (17-2)

Раскроем предыдущую формулу, подставив в нее РКЧХ объекта и регулятора, в результате получим:

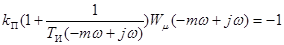. (17-3)

Разобьем полученное уравнение на уравнения для действительной и мнимой части, в результате получим:

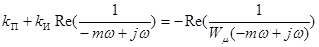; (17-4)

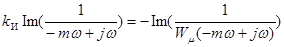. (17-5)

Из полученных уравнений выразим параметры настройки и получим:

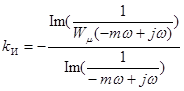; (17-6)

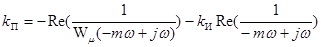. (17-7)

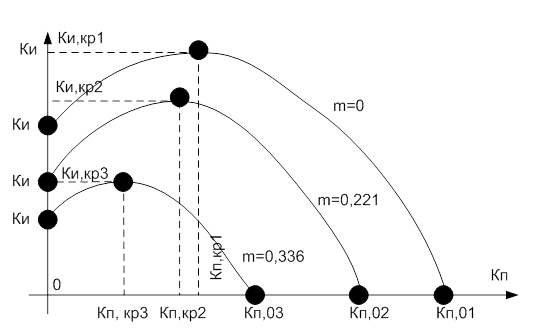
На основании полученных формул можно построить линии границы областей заданного запаса устойчивости на плоскости Ки-Кп (см. рис. 17-1).

Рис. 17-1. Линии границы области заданного запаса устойчивости в плоскости Ки-Кп.

Таким образом, при расчете АСР на минимум линейного интегрального показателя оптимальным настройкам ПИ-регулятора соответствуют точки максимума Ки, оптимальным настройкам И и П-регуляторов соответствуют точки на осях Ки и Кп соответственно.

При данных настройках расширенная КЧХ разомкнутой АСР проходит через точку -1,j0.