Инерционное звено второго порядка

Также в отдельных случаях называется колебательным или К-звеном. Примером физической реализации данного звена может являться система из двух сообщающихся баков с водой без насосов на стоке и притоке, если входом является перемещение клапана на притоке, а выходом - уровень во втором баке.

Дифференциальное уравнение инерционного звена второго порядка имеет вид, приведенный ниже: .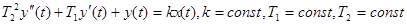

Коэффициент передачи данного звена обозначается k и имеет размерность, равную отношению размерности выходного сигнала к размерности входного. Т₁ и Т₂ - это постоянные времени звена, соответственно, они имеют размерность времени.

Передаточная функция звена имеет вид: .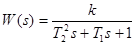

КЧХ звена имеет вид: .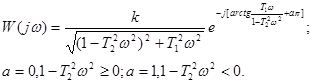

АЧХ звена имеет вид: .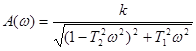

ФЧХ ИД-звена имеет вид: .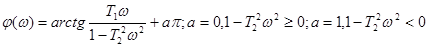

Вид переходной характеристики инерционного звена второго порядка зависит от вида корней характеристического уравнения звена, то есть, от соотношения постоянных времени Т₁ и T₂.

Если корни действительные и различные (-α₁;-α₂), то переходная характеристика имеет вид:

.

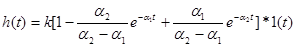Если корни вещественные и равные (-α), то переходная характеристика будет иметь вид:

.

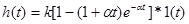Если корни являются комплексно-сопряженными (-α±jω)

.

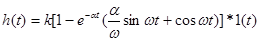В последнем случае переходная характеристика имеет колебательный характер.

Для систем с колебательностью также характерен пик на АЧХ на частоте колебаний. Затухание колебаний можно характеризовать корневым показателем колебательности, частотным показателем колебательности или степенью затухания.

Звено запаздывания

Также называется З-звеном. Примером физической реализации данного звена может являться транспортер.

Переходная характеристика З-звена имеет вид: .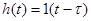

КЧХ З-звена имеет вид: .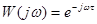

АЧХ З-звена имеет вид: А(ω)=1.

ФЧХ З-звена имеет вид: φ(ω)=-ωτ.

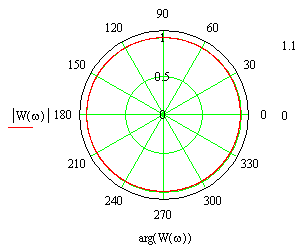
Вид годографа КЧХ З-звена приведен на рис. 9-10.

Рис. 3-20. Пример годографа КЧХ звена запаздывания.