Апериодическое звено первого порядка

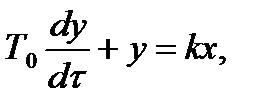
Дифференциальное уравнение апериодического звена – оригинал имеет вид

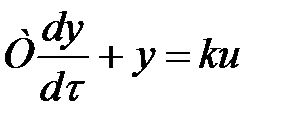. (5.2)

После преобразования по Лапласу уравнения (5.2) получим

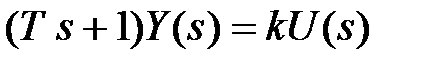. (5.3)

Здесь Т- постоянная времени; k – коэффициент передачи.

Из выражения (5.3) можно получить передаточную функцию

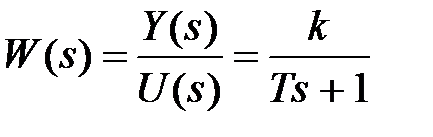. (5.4)

Аналитическое выражение вектора АФЧХ получают через передаточную функцию, заменив в ней оператор Лапласа s на выражение jw, где w – частота колебаний, w = 1/T₀; Т ₀ – период колебаний.

Тогда после необходимых преобразований (5.4) получим частотную характеристику:

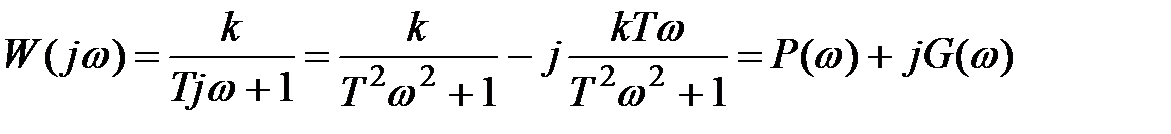. (5.5)

Изменяя частоту от 0 до ∞, можно построить (рис. 5.2) АФЧХ, т.е. годограф функции 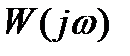, представляющий собой полуокружность, расположенную в четвертом квадранте комплексной плоскости, диаметр которой равен коэффициенту k.

Рис. 5.2. График АФЧХ апериодического звена.

На рис. 5.3. показана АЧХ, представляющую кривую описываемую равенством

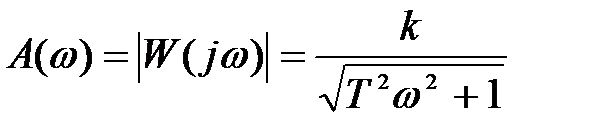. (5.6)

Кривая ФЧХ (рис. 5.3, б) описывается равенством

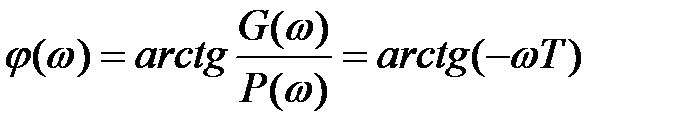. (5.7)

Рис. 5.3. Графики АЧХ и ФЧХ апериодического звена первого порядка

На рис. 5.4 приведена типовая кривая разгона апериодического звена, которая называется экспонентой. Если к любой ее точке провести касательную, а затем точку касания и точку пересечения касательной с асимптотой, спроецировать на ось времени, то получится один и тот же отрезок на оси времени. Эта проекция, называемая постоянной времени, соответствует коэффициенту Т в передаточной функции, а ордината асимптоты, к которой стремится экспонента соответствует коэффициенту k.

Рис. 5.4. Переходная функция апериодического звена.

Таким образом по переходной функции легко найти коэффициента k и Т в передаточной функции апериодического звена. Если известная осциллограмма переходной функции получена экспериментально, то выделив на графике точку h = 0,63, принимая k = 1 получим t = T.

Чтобы получить выражение для построения логарифмической амплитудно-частотной характеристики в формулу (4.10) подставим равенство (5.6), тогда имеем

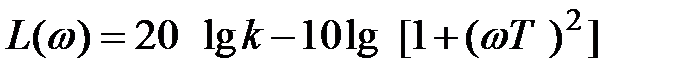. (5.8)

При построении графика вначале составим уравнение низкочастотных асимптот, которое получиться при 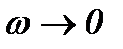и wТ₀ < 1 в виде

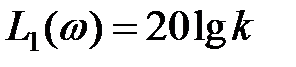. (5.9)

Уравнение высокочастотных асимптот при 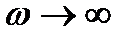и wТ > 1 получится из (5.8)

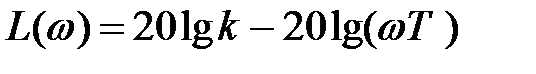(5.10)

Асимптота, построенная по зависимости (5.9) представляет прямую параллельную оси абсцисс, асимптота, построенная по равенству (5.10) представляет прямую с наклоном 20 дБ/дек. В чем нетрудно убедиться, взяв конкретные значения w. На рис. 5.5, a построена логарифмическая амплитудная характеристика при различных значениях k.

Чтобы построить логарифмическую фазовую характеристику в выражение (4.9) подставим в числитель и знаменатель, соответствующие слагаемые из (5. 5), тогда имеем

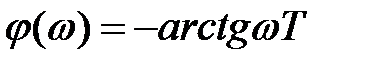(5.11)

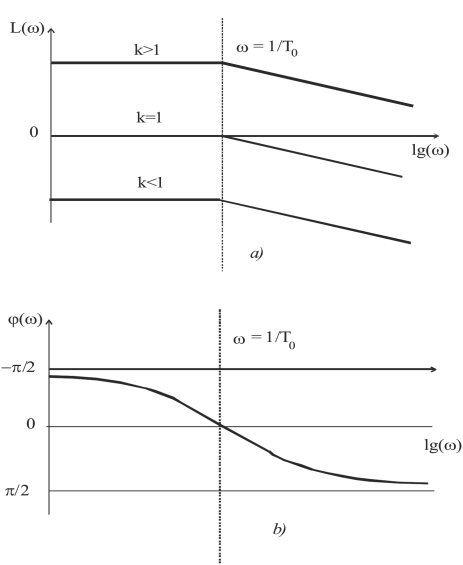
Рис. 5.5.Графики ЛАЧХ и ЛФХ апериодического звена

На рис.5.6, b построена логарифмическая фазовая характеристика. При этом по оси абсцисс откладывается значение lgw.

Примером реализации апериодического звена является электродвигатель небольшой мощности, который после включения в электросеть (подачи единичного скачка) набирает обороты по экспоненте. Другим примером является электрический RC. Объекты с передаточной функцией апериодического звена называются статическими.