Колебательное звено

Колебательным звеном может быть представлен элемент САУ, включающий не один, а два энергетические или массовые ёмкости. Например, в одной ёмкости накапливается потенциальная энергия, а в другой – кинетическая. Канал, по которой обмениваются энергией, обладает некоторым сопротивлением и на нем происходит потеря энергии. Мерой потери энергии является коэффициент затухания 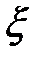. Причем чем больше 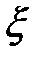, тем больше потери.

При 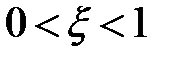переходной процесс будет колебательным и звено будет называться колебательным. Колебательное звено описывается дифференциальным уравнением вида

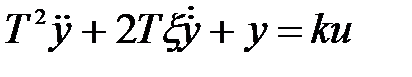(x>1) .(5.12)

После преобразования по Лапласу получим

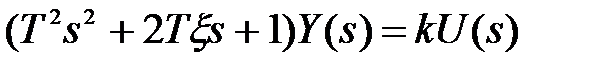(5.13)

Корни характеристического уравнения 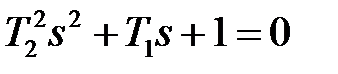должны быть комплексными, что будет выполняться при условии .

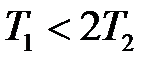Уравнение (5.13) обычно представляется в виде

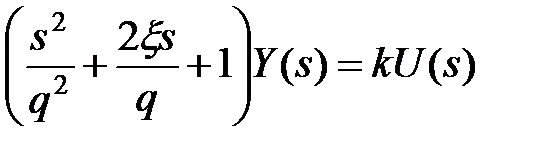, (5.14)

где 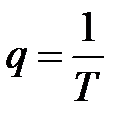– угловая частота свободных колебаний (при отсутствии затухания),

Передаточная функция колебательного звена имеет вид

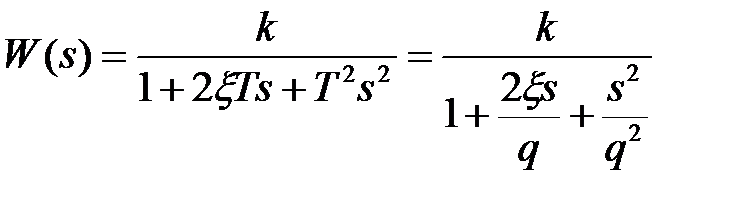. (5.15)

Примерами колебательного может быть виброзащитная система (демпфер), RLC-цепи, управляемые двигатели постоянного тока (при определенных условиях), упругие механические передачи, гироскопические устройства.

Корни характеристического уравнения для ДУ (5.12) будут при 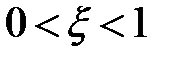комплексные сопряженные с отрицательной вещественной частью

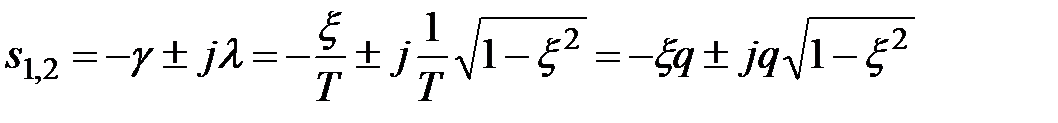. (5.16)

Вещественная часть корня 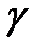представляет собой коэффициент затухания переходного процесса, а 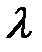– частоту затухающих колебаний.

Переходная характеристика колебательного звена описывается следующим уравнением:

,

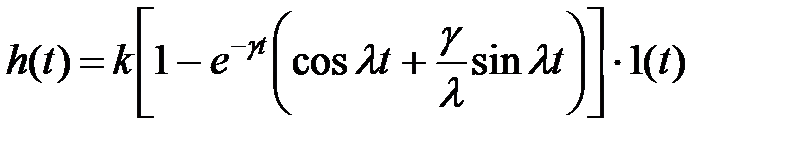где 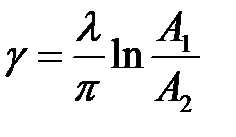; ; 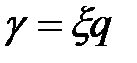; 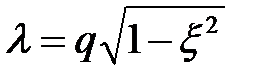А₁,А₂ – максимальные амплитуды колебаний относительно его установившегося значения, отстоящие друг от друга на время, равное полупериоду колебаний.

График переходной характеристики носит колебательный характер и представлен на рис. 5.7.

Импульсная переходная характеристика колебательного звена описывается следующим уравнением:

,

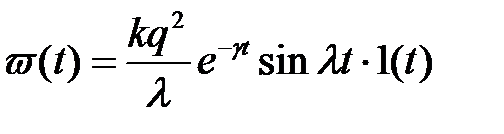где ; ; .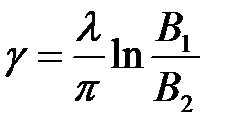

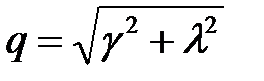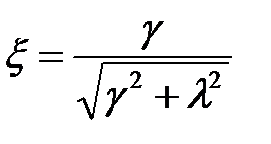Рис. 5.7. Переходная характеристика колебательного звена

График импульсной переходной характеристики носит колебательный характер и представлен на рис. 5.8.

Рис. 5.8. Импульсная переходная характеристика колебательного звена

График амплитудной фазовой частотной характеристики колебательного звена показан на рис. 5.9.

Амплитудная частотная характеристика (Рис. 5.10) может иметь резонансный пик и описывается уравнением вида

.

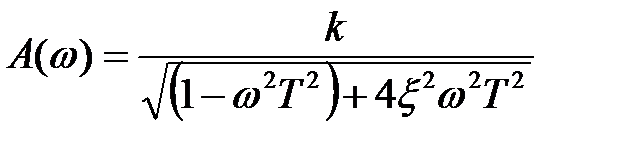Рис. 5.9. График АФЧХ колебательного звена

Исследование модуля частотной передаточной функции на максимум показывает, что пик будет существовать при 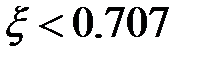. Высота пика будет тем больше, чем меньше параметр затухания:

.

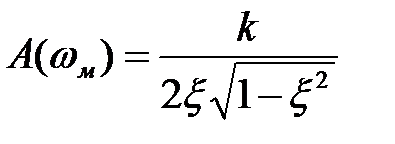Максимум амплитудной частотной характеристики соответствует частоте

.

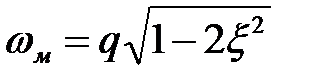Рис. 5.10. График АЧХ колебательного звена

Фазовая частотная характеристика колебательного звена (Рис. 5.11) описывается уравнением вида

.

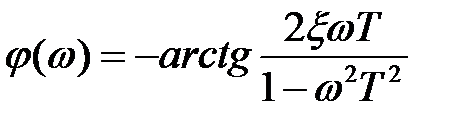Рис. 5.11. ФЧХ колебательного звена

Логарифмическая амплитудная частотная характеристика строится по выражению

,

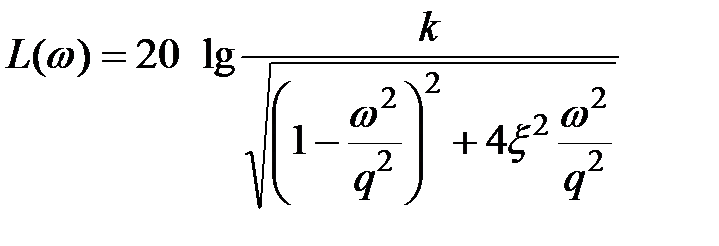и имеет вид представленный на рис. 5.12.

Рис. 5.12. График ЛАЧХ колебательного звена

Снижение параметра затухания 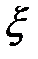приводит к повышению колебательности переходного процесса и росту резонансного пика амплитудной частотной характеристики.

В идеальном случае 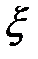= 0, это означает, что потери энергии отсутствуют. Так как звено сохраняет первоначальный запас энергии, переходной процесс будет незатухающим.

В том случае, когда 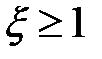, то потери энергии будут настолько велики, что переходной процесс не будет колебательным. Звено в этом случае назывется апериодическим второго порядка. Передаточная функция такого звена может быть представлена в виде

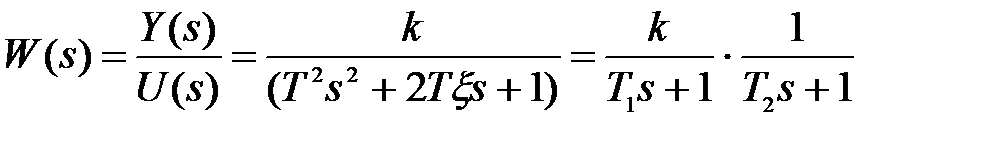, (5.17)

из которого следует, что апериодическое звено второго порядка можно представить как последовательно соединенные два апериодических звена первого порядка.