Интегродифференцирующее звено

Также называется ИД-звеном.

Дифференциальное уравнение интегродифференцирующего звена имеет вид, приведенный ниже: .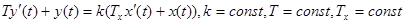

Коэффициент передачи ИД-звена обозначается k и имеет размерность, равную отношению размерности выходного сигнала к размерности входного. Т и Т_х - это постоянные времени ИД-звена, соответственно, они имеют размерность времени.

Передаточная функция ИД-звена имеет вид: .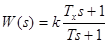

КЧХ ИД-звена имеет вид: .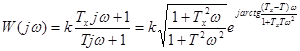

АЧХ ИД-звена имеет вид: .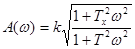

ФЧХ ИД-звена имеет вид: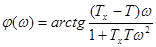

Переходная характеристика ИД-звена имеет вид: .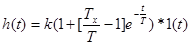

Импульсная переходная характеристика ИД-звена: .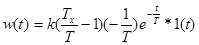

Как видно из приведенных выше формул, вид характеристик ИД-звена зависит от соотношения Т и Т_х. Приведем вид характеристик для случая Т>T_x.

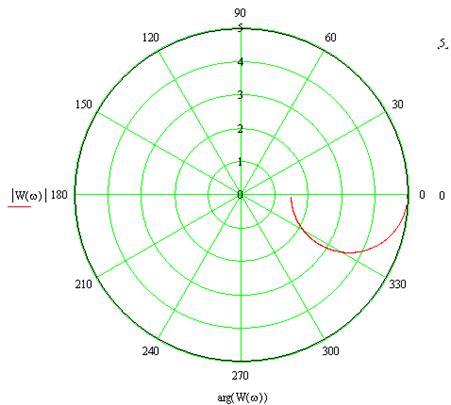
Вид КЧХ ИД-звена приведен на рис. 9-6. Т=10, Т_х=3, k=5. Как видно, в данном случае начинается на вещественной положительной полуоси в точке с координатой k, далее идет в сторону уменьшения вещественной части в точку с координатой kT_x/T и представляет собой полуокружность.

Рис. 3-16. Пример годографа КЧХ ИД-звена.

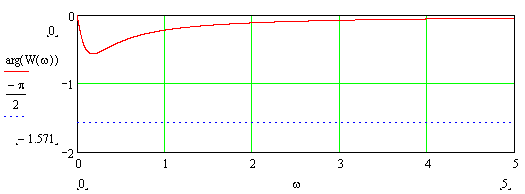
Пример ФЧХ для данного случая приведен на рис. 9-7.

Рис. 3-17. Пример ФЧХ ИД-звена.

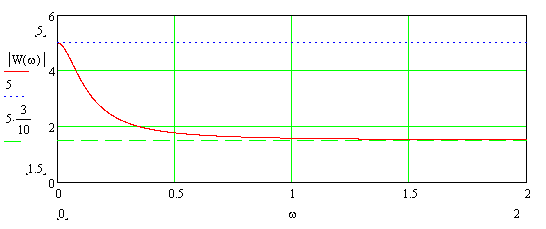
Пример АЧХ для данного случая приведен на рис. 9-8. Как видно из графика и приведенной формулы, при нулевой частоте она начинается на оси ординат в точке с координатой k, монотонно убывает и при увеличении частоты асимптотически приближается к горизонтальной прямой kT_x/T.

Рис. 3-18. Пример АЧХ ИД-звена.

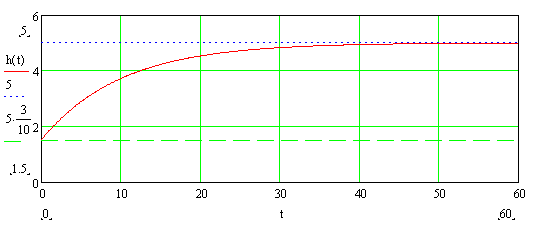
Пример переходной характеристики ИД-звена для данного случая приведен на рис. 9-9. Как видно из рисунка и приведенной выше формулы график начинается на оси ординат в точке с координатой kT_x/T и с течением времени, монотонно возрастая, асимптотически приближается к горизонтальной прямой с координатой k.

Рис. 3-19. Пример переходной характеристики ИД-звена.