Типовые структуры моделей объектов управления

Модель объекта может быть получена аналитически или экспериментально. При аналитическом получении моделей они записываются в виде дифференциальных уравнений на основании законов физики и т.д. При экспериментальном получении моделей их получают на основании экспериментального графика или таблицы чисел.

Принятая структура математической модели передаточной функции объекта – дробно-рациональная функция и звено запаздывания:

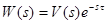. (12-1)

Существуют объекты с самовыравниванием и без самовыравнивания. При моделировании объекта с самовыравниванием обычно используют цепочку А-звеньев последовательно со звеном запаздывания, передаточная функция имеет вид:

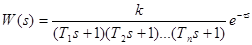. (12-2)

Объекты без самовыравнивания моделируются цепочкой апериодических звеньев, последовательно с которой включено И-звено и З-звено, передаточная функция имеет вид:

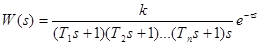. (12-2)

Простейший вид модели для объекта с самовыравниванием имеет вид:

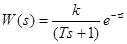. (12-4)

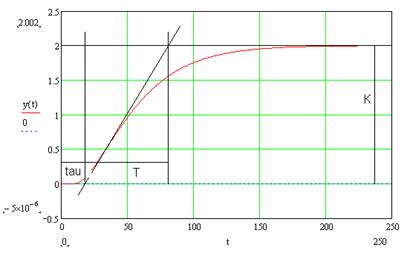
Как видно, в данном случае модель объекта представляет собой последовательное соединение апериодического звена и звена запаздывания. Способ нахождения параметров модели объекта представлен на рис. 12-1. Для того, чтобы найти параметры, необходимо провести касательную к точке перегиба переходной характеристики объекта.

Рис. 12-1. Нахождение параметров простейшей модели объекта.

Если полученная точность не удовлетворительна, необходимо усложнить модель.

Следует заметить, что переходная характеристика определяет поведение объекта только в линейном приближении, то есть, вид модели зависит от точки линеаризации, для увеличения точности нужно рассмотреть несколько точек, то есть, снять переходные характеристики в нескольких режимах. Кроме того, экспериментально снятая переходная характеристика фактически является оценкой, то есть, случайной функцией времени, поэтому для повышения точности следует снять несколько реализаций при одном режиме и усреднить по множеству.