Звенья с распределенными параметрами

В состав тепловых объектов часто входят элементы, аккумулирующие емкости в которых имеет распределенный характер. Динамические процессы в таких элементах описываются уравнениями в частных производных. Передаточные функции таких объектов являются трансцендентными функциями s.

Примером объекта с распределенными параметрами является звено запаздывания.

Основные понятия имитационного моделирования. Разностные уравнения

Выражение для y(t) не всегда можно найти путем решения дифференциального уравнения или через преобразования Фурье и Лапласа или через интеграл свертки.

Это происходит потому, что не всегда можно получить математическое описание объекта в явном виде и линеаризовать. Кроме того, исследуемый объект может быть подвержен одновременному действию нескольких возмущений, поступающих на различные входы. Возмущения могут быть различного характера, в том числе, случайные.

В описанных случаях можно применять имитационное моделирование, то есть, численное решение дифференциальных уравнений (для дифференциальных уравнений первого порядка – метод Эйлера).

Например, для апериодического звена можно записать:

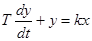; (12-5)

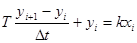. (12-6)

Из последней формулы можно с помощью арифметических преобразований выразить y_i+1. Полученная формула носит название рекуррентной и для А-звена имеет вид:

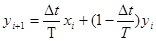. (12-7)

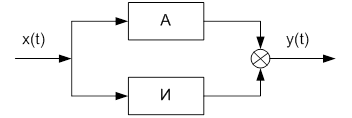
Аналогичные формулы могут быть получены для всех элементарных звеньев. Далее модель объекта может быть "набрана" из элементарных звеньев, как из блоков. Пусть имеется система, показанная на рис. 12-2.

Рис. 12-2. Параллельное соединение А и И-звеньев.

При реализации в программе MathCad формулы для данного случая будут иметь вид:

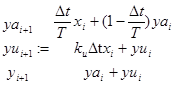. (12-8)