Взаимосвязь между параметрами состояния среды до и после фронта УВ определяется законами сохранения массы, количества движения (импульса) и энергии.
1. Уравнение сохранения массы
В момент времени t = 0 в сечении 0-0 поршень мгновенно начал движение со скоростью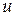 
. За время t поршень перемещается на расстояние 
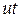в сечение 1-1, при этом от поршня в невозмущенный газ начинает распространяться фронт УВ (2-2) со скоростью D, большей, чем 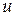. Ударная волна за время t прошла расстояние 
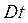. Расстояние между поршнем и УВ стало 
.
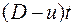Объем сжатого газа равен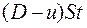 
, а первоначальный объем того же количества газа был равен 
.
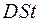Масса сжатого газа равна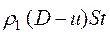 
, а масса газа перед сжатием 
.
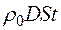По закону сохранения массы, масса вещества не изменяется:
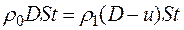, (3.1)
или
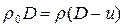. (3.2)
2. Уравнение сохранения количества движения (импульса)
Сжатый газ движется со скоростью поршня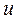 
. Следовательно, при сжатии масса 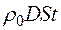приобретает количество движения (импульс) 
.
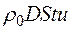По второму закону Ньютона изменение количества движения равно импульсу силы, т.е. произведению силы на время ее действия: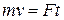 
.
Этот импульс (за время t) равен импульсу сил давления
= 
.
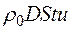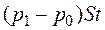откуда получаем
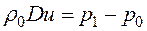. (3.3)
3. Уравнение сохранения энергии.
Принимается, что при сжатии газ не отдает и не получает тепла извне. Изменение энергии газа при сжатии равно работе внешней силы, перемещающей поршень за время t.
Полная энергия складывается из внутренней (тепловой) энергии и кинетической энергии движущегося газа.
Обозначим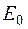 
и 
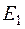начальную и конечную удельную внутреннюю энергию единицы массы. Кинетическая энергия сжатого газа равна 
.
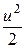Приращение энергии для единицы массы газа равно
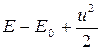, (3.4)
где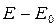 
- приращение внутренней энергии;
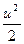- приращение кинетической энергии единицы массы вещества.
При давлении на поршень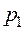 
который перемещается на расстояние 
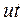, работа внешней силы равна
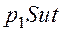. (3.5)
Т.к. масса газа равна 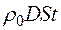, то полное изменение энергии газа при сжатии равно
.
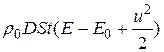По закону сохранения энергии приравниваем изменение энергии работе силы
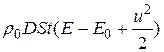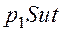= , (3.6)
и сокращая на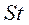 
, получаем
= 
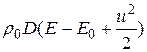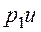. (3.7)
Дата добавления: 2017-08-01; просмотров: 738;