Вибрация механической системы с распределенными параметрами при внешней периодической нагрузке.
Рассмотрим систему с распределенными параметрами, допускающую получение аналитического решения.
В качестве примера рассмотрим трубопровод, находящийся под воздействием сил инерции, упругой реакции материала трубы, демпфирования и внешней периодической нагрузки. Считаем, что трубопровод представляет собой балку на двух опорах. Как и выше, используем модель вязкого демпфирования. Уравнение движения системы будет иметь вид
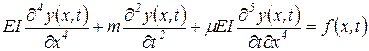 , ,
| (87) |
где f(x,t) - внешняя нагрузка.
Решение этого уравнения в явной форме состоит из двух частей:
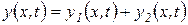 , ,
|
где 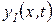 ‑ общее решение однородного уравнения (без правой части);
‑ общее решение однородного уравнения (без правой части);
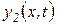 ‑ частное решение неоднородного уравнения (с правой частью).
‑ частное решение неоднородного уравнения (с правой частью).
На основании изложенного выше считаем, что решение 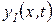 определяет свободные колебания системы, зависящие от начальной формы искривления и от скоростей, сообщаемых в начальный момент времени элементам системы. Эти колебания вследствие наличия демпфирования затухают со временем и остаются лишь вынужденные колебания. Рассмотрим решение
определяет свободные колебания системы, зависящие от начальной формы искривления и от скоростей, сообщаемых в начальный момент времени элементам системы. Эти колебания вследствие наличия демпфирования затухают со временем и остаются лишь вынужденные колебания. Рассмотрим решение 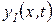 .
.
Рассмотрим случай жесткого закрепления концов. Определим выражение для фундаментальных функций Хn.
Введем новые обозначения для фундаментальной функции
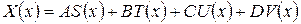 ,
,
где А, В, С, D ‑ постоянные интегрирования.
S(x), Т(х), U(x) V(x) ‑ Функции Крылова, определяемые по выражениям:
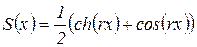 ;
; 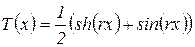 ;
;
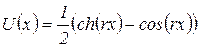 ;
; 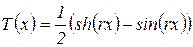 ;
;
При использовании функций Крылова полезно иметь в виду следующие их свойства:
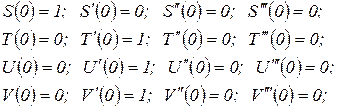
Производные от функций Крылова приведены в табл. 10.
Таблица 10
Производные от функций Крылова
| Функция | Первая | Вторая | Третья | Четвертая |
| S | rV | r2U | r3Т | r4S |
| Т | rS | r2V | r3U | r4T |
| U | rТ | r2S | r3V | r4U |
| V | rU | r2T | r3S | r4V |
Функции Крылова позволяют сразу написать общий интеграл, удовлетворяющий граничным условиям на конце х=0. Для жесткого закрепления концов трубопровода длиной l
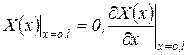 . .
|
Тогда общий интеграл уравнения для фундаментальных функций будет иметь вид
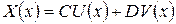 , ,
| (88) |
который удовлетворяет всем граничным условиям при х=0:
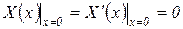 . .
|
Постоянные С и D находим из условия на конце х=1:
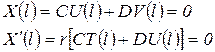 . .
| (89) |
Данная система уравнений является однородной относительно неизвестных С и D. Чтобы она имела решения, отличные от нуля, коэффициент r должен иметь значения, приведенные в параграфе 2.2, для соответствующего условия закрепления.
Уравнение соответствующей собственной формы составим следующим образом. Из первого или второго уравнения (89) получаем
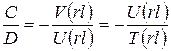 . .
| (90) |
Подставив отношение (90) в уравнение форм колебаний (88), получим
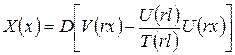 . .
|
Отсюда следует, что собственная форма колебании определяется с точностью до постоянного множителя.
Теперь рассмотрим случай воздействия на систему внешней сосредоточенной гармонической нагрузки 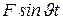 приложенной в точке х=а.
приложенной в точке х=а.
Для этого случая имеем
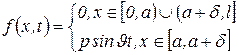 . .
| (91) |
при условии, что 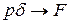 когда
когда 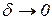 .
.
Решение уравнения (87) будем искать по методу А.Н.Крылова в виде разложения в ряд по фундаментальным функциям 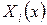 , получаемым для балки без учета затухания
, получаемым для балки без учета затухания
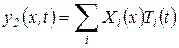 , ,
| (92) |
где функции 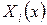 зависят от условий закрепления концов трубопровода-балки.
зависят от условий закрепления концов трубопровода-балки.
Подставляя 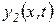 в виде (92) в уравнение (87), выраженное в безразмерных координатах
в виде (92) в уравнение (87), выраженное в безразмерных координатах
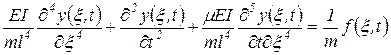 , ,
| (93) |
и принимая во внимание, что
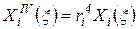 , ,
| (93) |
получим
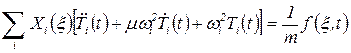 , ,
|
где 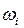 - собственная частота, соответствующая i-му тону.
- собственная частота, соответствующая i-му тону.
Умножая обе части последнего выражения на 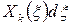 и интегрируя в пределах от 0 до 1, получим
и интегрируя в пределах от 0 до 1, получим
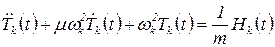 , ,
|
где
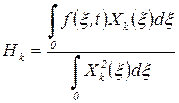 , ,
|
так как вследствие условия ортогональности для фундаментальных функций в левой части все члены, содержащие произведение функций 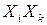 , пропадут.
, пропадут.
Для
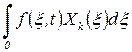 , ,
|
получим, согласно условию (91) 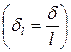
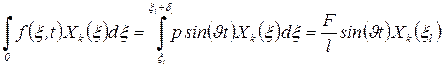 . .
|
Значение
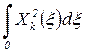 . .
|
может быть взято из табл. 11.
Таблица 11
Значения 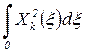 интегралов при различных видах условий закрепления
интегралов при различных видах условий закрепления
| х=0 | х=1 | I | II |
| Заделан | Заделан | 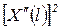
| 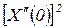
|
| Оперт | Оперт | 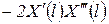
| 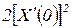
|
Таким образом, для 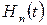 после разложения получим следующие значения:
после разложения получим следующие значения:
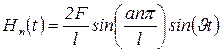 - для идеального шарнирного опирания обоих концов;
- для идеального шарнирного опирания обоих концов;
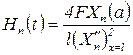 для идеально жесткого закрепления обоих концов.
для идеально жесткого закрепления обоих концов.
Тогда для чисто вынужденных колебаний согласно решению уравнения (87) соответственно получим:
идеальное шарнирное опирание обоих концов:
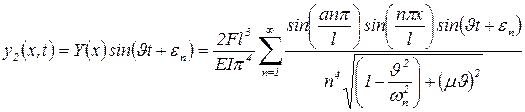 ; ;
| (94) |
идеально жесткое закрепление обоих концов:
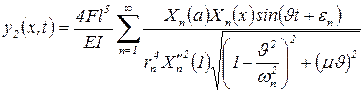 , ,
| (95) |
где 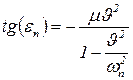
Из выражений (94) и (95) следует, что амплитуда вынужденной вибрации достигает своего максимального значения при выполнении условия
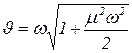 , ,
| (96) |
Поэтому в механической системе с распределенными параметрами без демпфирования, то есть 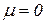 , если частота внешней возмущающей нагрузки стремится к одной из частот собственных колебаний
, если частота внешней возмущающей нагрузки стремится к одной из частот собственных колебаний 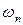 , то амплитуда вынужденных колебаний неограниченно возрастает.
, то амплитуда вынужденных колебаний неограниченно возрастает.
Если система обладает демпфированием 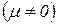 , то при выполнении условия (96) амплитуда гармонических колебаний механической системы достигает своего максимального значения, но ее величина ограничена и является функцией коэффициента демпфирования
, то при выполнении условия (96) амплитуда гармонических колебаний механической системы достигает своего максимального значения, но ее величина ограничена и является функцией коэффициента демпфирования 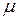 .
.
Таким образом, принципиальные выводы относительно условий резонанса и закона движения механической системы под действием внешней возмущающей периодической нагрузки одномассовой и многомассовой механических систем и системы с распределенными параметрами в условиях резонанса совпадают.
Выводы.
На основе рассмотренных примеров анализа движения системы под воздействием внешней гармонической нагрузки можно сделать следующие выводы:
· под внешней к рассматриваемой механической системе нагрузкой понимаем нагрузку, параметры которой не зависят от функций перемещений точек системы и их производных;
· при воздействии на механическую систему внешней гармонической нагрузки возможно появление условий резонанса. Поэтому одной из возможных причин потери устойчивости или, по крайней мере, повышенного уровня вибрации может являться внешняя нагрузка;
· если механическая система не обладает демпфированием, то условие резонанса характеризуется совпадением частоты внешней гармонической нагрузки с одной из собственных частот системы. Если же механическая система обладает демпфированием, то значение резонансной частоты не совпадает с собственной частотой системы;
· причиной вибрации может быть самостоятельное (например, сейсмическое) перемещение опор (математически выраженное переменными по времени функциями, соответствующими граничным условиям);
· точное значение спектра собственных частот необходимо для исключения условий возникновения резонанса (отстройки от резонанса). Это значит, что отстройка от резонанса является одним из методов борьбы с повышенным уровнем вибрации или обеспечения динамической устойчивости механической системы;
· использование обобщенных масс и жесткости позволяет описать движение каждой массы многомассовой системы уравнением движения одномассовой системы.
Причинами повышенного уровня вибрации являются:
· внешняя гармоническая нагрузка;
· самостоятельное перемещение опор;
· сила Кориолиса.
Как показывает практика, основной источник возмущения трубопровода - транспортируемый поток. Воздействие потока на трубопровод характеризуется силами, количественно отражающими меру этого воздействия. В рассмотренных выше примерах учитывались лишь две количественные характеристики потока - масса потока на единицу длины трубопровода 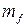 и скорость движения потока по трубопроводу
и скорость движения потока по трубопроводу 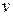 . Помимо этого, одной из основных количественных характеристик потоков газа, нефти и нефтепродуктов является давление транспортируемой среды р. Это значит, что в общем случае в числе силовых факторов, действующих на трубопровод со стороны потока, должны быть силы, определяемые давлением среды.
. Помимо этого, одной из основных количественных характеристик потоков газа, нефти и нефтепродуктов является давление транспортируемой среды р. Это значит, что в общем случае в числе силовых факторов, действующих на трубопровод со стороны потока, должны быть силы, определяемые давлением среды.
Кроме этого, в приведенных выше примерах рассматривался лишь прямолинейный трубопровод, в то время как реальная трубопроводная система в общем случае является пространственной системой со сложной геометрией (отличной от прямолинейной).
Уравнение движения трубопровода произвольной геометрии в пространстве с учетом давления потока без внешней нагрузки имеет вид
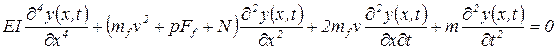
где:
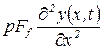 - сила давления транспортируемого потока;
- сила давления транспортируемого потока;
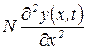 - осевые усилия в трубопроводе;
- осевые усилия в трубопроводе;
N - осевая сила статического натяжения труоопровода.
Отметим ряд принципиальных аспектов, связанных с использованием этой математической модели.
В рассматриваемом случае формально трубопровод не подвержен воздействию внешней возмущающей нагрузки. Однако это не значит, что трубопровод совершает только собственные колебания. Силы, определяющие воздействие транспортируемого потока на трубопровод зависят от перемещений трубопровода и их производных. Поэтому эти силы стоят в левой части уравнения движения. Но именно движущийся по трубопроводу поток вызывает его вынужденную вибрацию.
Численные характеристики потока (вынуждающей силы) входят в коэффициенты слагаемых, расположенных в левой части уравнения движения. Следовательно, собственные частоты трубопровода являются функциями численных характеристик потока (вынуждающей силы).
Одной из причин вибрации механической системы является периодический характер изменения коэффициентов, т. е. численные характеристики потока являются периодическими функциями. Таким образом, периодическое изменение численных характеристик потока 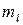 ,
, 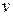 и
и 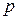 (пульсация потока) является следующей причиной вибрации трубопроводных систем.
(пульсация потока) является следующей причиной вибрации трубопроводных систем.
Итак, повышенный уровень вибрации механической системы приводит к росту амплитуды перемещения точек системы или даже к потере устойчивости.
В связи с этим возникает вопрос о допустимых уровнях вибрации механической системы.
3.5. Задание для самостоятельной работы
Получить уравнение упругой линии трубопровода под действием внешней гармонической нагрузки, приложенной на расстоянии а от левой опоры.
Параметры внешней нагрузки (одна гармоника) взять из задания для самостоятельной работы 1.5.
Условия закрепления взять из задания для самостоятельной работы 2.7.
Дата добавления: 2018-09-24; просмотров: 1196;
