Собственные колебания механической системы с распределенными параметрами с учетом демпфирования

Как видно из представленных на рис.8 и рис.9 графиков, изменение геометрических размеров трубы, а следовательно ее жесткости и массы, а также плотности транспортируемого продукта может привести к принципиальному изменению численного значения собственной частоты даже в предельно упрощенном варианте расчетной схемы (рассматриваются всего два силовых фактора).

Но реальные системы находятся в более сложных условиях нагружения, что ведет к необходимости учета при анализе технического состояния большего количества силовых факторов и более сложных условий закрепления, чем рассмотренные в предыдущем примере. Рассмотрим влияние на численные значения собственных частот механической системы таких реально действующих силовых факторов, как упругая реакция грунта (для подземных и проложенных по поверхности земли трубопроводов) и демпфирование.

Рассмотрим самый простой вариант расчетной схемы, то есть будем считать, что трубопровод-балка находится под воздействием сил собственного веса, упругой реакции материала трубы и реакции грунта. В качестве модели грунта рассмотрим вариант упругого основания. Таким образом, в качестве расчетной схемы проложенного по поверхности земли трубопровода используем балку на упругом основании. Тогда уравнение движения трубопровода будет иметь вид

.

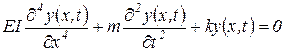(33)

где k - коэффициент упругой податливости основания (грунта);

kу(х,t) - сила упругой реакции основания (грунта).

После введения безразмерной координаты x=x/l уравнение (33) примет вид

.

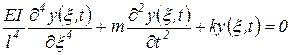(33)

Введем обозначения

, .

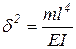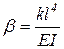Тогда последнее уравнение можно представить в виде

.

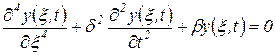(34)

Согласно методу Фурье, решение уравнения (34) следующие:

,

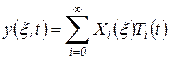(34)

в котором функции формы и времени не равны тождественно нулю. Подставим искомое решение в виде (35) в уравнение (34). Получим уравнения для каждого слагаемого в выражении (35), поэтому индекс i опускаем,

.

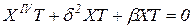Вынесем не равные тождественно нулю функции формы и времени за скобки и получим, что

.

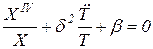(36)

После элементарного преобразования находим

.

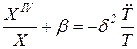Левая часть последнего равенства является функцией безразмерной координаты x, а правая часть - функцией времени t. Поэтому левая и правая части должны быть равны постоянной величине, которую обозначим как r⁴. Таким образом вместо одного уравнения (36) относительно двух переменных x и t имеем два уравнения, каждое из которых является уравнением относительно одного переменного соответственно x и t. Эквивалентная (36) система уравнений имеет вид

.

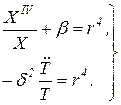(37)

Уравнения системы (37) можно переписать в виде

.

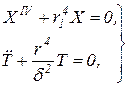(38)

где

.

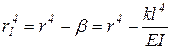В технической диагностике принято использовать следующее обозначение:

.

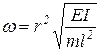(39)

которое совпадает с выражением (32).

Первое уравнение системы (38), определяющее функцию формы, фактически идентично (29) и отличается лишь численным значением постоянной величины r⁴.

Функция времени находится из второго уравнения системы (38) и согласно изложенному выше материалу определяется по выражению

,

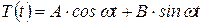(39)

которое аналогично выражению функции времени в (28).

Таким образом, усложнение расчетной схемы за счет замены двух расположенных по концам трубопровода опор упругим основанием не изменило значений собственных частот трубопровода, но привело к изменению функции формы за счет изменения численного значения коэффициента в аргументе функции формы.

Рассмотрим влияние демпфирующих свойств механической системы на спектр собственных частот. При этом для простоты вычислений в качестве сил демпфирования учитываем лишь внутреннее трение материала трубы и не учитываем внешнего затухания.

Поскольку силы демпфирования нельзя оценить с такой же точностью, как силы упругой реакции и силы инерции, то строгое математическое моделирование демпфирования невозможно. Тем не менее для объяснения диссипативных сил конструкции следует сделать предположение о виде демпфирования, что позволяет оценить демпфирующие силы на практике. Кроме того, вид демпфирования должен соответствовать простым математическим операциям, используемым для анализа линейных уравнений движения ‑ это означает, что при гармоническом возбуждении силы демпфирования также должны изменяться по гармоническому закону. Двумя такими формами демпфирования являются вязкое и гистерезисное демпфирование. В данном случае используем модель вязкого демпфирования, согласно которой сила демпфирования пропорциональна мгновенной скорости.

При данной расчетной схеме (учитываем три силовых фактора) уравнение движения трубопровода с учетом введения безразмерной координаты будет иметь вид

.

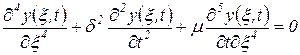(40)

где m - коэффициент, характеризующий внутреннее трение материала, в данном случае играющий роль коэффициента демпфирования;

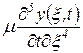- сила демпфирования.

Решение уравнения (40) найдем способом, аналогичным нахождению решения уравнения (34). После подстановки искомого решения в виде (35) и проведения аналогичных уравнению (34) преобразований вместо уравнения (36) получим следующее уравнение

,

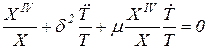(41)

которое после несложных преобразований приводится к виду

,

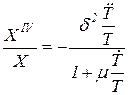Левая и правая части последнего уравнения являются функциями разных переменных соответственно x и t и поэтому должны равняться одной и той же постоянной величине, которую обозначим как r⁴. Тогда вместо одного уравнения (40) имеем систему двух уравнений, каждое из которых является уравнением относительно одной переменной соответственно x и t

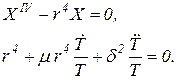
Первое уравнение для функции формы аналогично (29) и его решение находится по выражению (31). Введя обозначение, аналогичное (39), второе уравнение для функции времени можно привести к виду

,

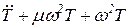где w - собственная частота колебаний трубопровода-балки без затухания, определяемая по формуле (39).

Решение данного уравнения и, следовательно, функция времени зависят от соотношения между коэффициентами. Согласно изложенному выше, функция времени будет иметь вид

.

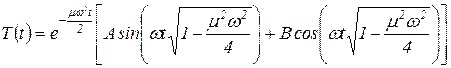(42)

Таким образом, частота собственных колебаний трубопровода-балки с учетом демпфирования

.

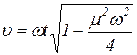(43)

Обычно m малая величина. В этом случае значение частоты собственных колебаний при учете затухания может быть принято равным

.

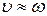Для случая

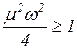
движение является апериодическим, что может привести к потере трубопроводом своей устойчивости, то есть сопровождаться неограниченным ростом численного значения параметров системы. В рассматриваемом случае потеря устойчивости означает неограниченный рост перемещения точек трубопровода, что неизбежно приведет к аварии. Полученный результат приводит к вопросу о том: может ли коэффициент демпфирования или, в более общей постановке, коэффициент при слагаемом в уравнении движения трубопровода, содержащим первую производную по времени, достигать значения, при котором движение системы может стать апериодичным.