Потеря устойчивости трубопровода вследствие силы Кориолиса.
Для ответа на поставленный в предыдущем параграфе вопрос, рассмотрим случай трубопровода постоянного сечения, транспортирующего поток жидкости или газа. В качестве силовых факторов рассматриваем силу инерции трубопровода, силу упругой реакции материала трубы, силу инерции потока, движущегося по криволинейной траектории, и силу инерции, связанную с кориолисовым ускорением.
В рамках принятой расчетной схемы дифференциальное уравнение трубопровода с потоком жидкости или газа имеет вид
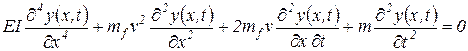 , ,
| (44) |
где v - постоянная средняя скорость течения потока относительно трубы;
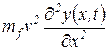 - сила инерции потока, движущегося по криволинейной траектории;
- сила инерции потока, движущегося по криволинейной траектории;
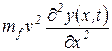 - сила инерции потока, связанная с кариолисовым ускорением (сила Кариолиса).
- сила инерции потока, связанная с кариолисовым ускорением (сила Кариолиса).
Таким образом, мы увеличили число учитываемых при анализе состояния трубопровода численных характеристик транспортируемого потока до двух – 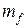 и v.
и v.
Рассмотрим влияние силы инерции потока, связанной с кориолисовым ускорением. Для этого найдем решение уравнения (44).
Из характеристического уравнения следует, что решение уравнения (44) имеет вид
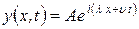 . .
| (45) |
Для исследования решения уравнения (44) и определения собственных частот используем метод Галеркина, заключающийся в представлении решения в виде суммы собственных форм. Рассмотрим первые две формы поперечной вибрации идеального шарнирно опертого в обеих опорах трубопровода длиной l. Для этого примем функцию прогиба трубопровода в виде
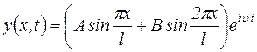 . .
| (46) |
Подставив функцию прогиба в виде (46) в уравнение (44), умножив затем полученное выражение поочередно на 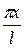 и на
и на 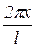 и проинтегрировав по длине трубопровода l, получаем систему двух линейных уравнений относительно неизвестных постоянных А и В. Приравняв к нулю определитель из коэффициентов этой системы, после упрощений получим уравнение, определяющее собственные частоты рассматриваемой механической системы. Определив корни последнего уравнения, получаем зависимости для первых двух собственных частот
и проинтегрировав по длине трубопровода l, получаем систему двух линейных уравнений относительно неизвестных постоянных А и В. Приравняв к нулю определитель из коэффициентов этой системы, после упрощений получим уравнение, определяющее собственные частоты рассматриваемой механической системы. Определив корни последнего уравнения, получаем зависимости для первых двух собственных частот
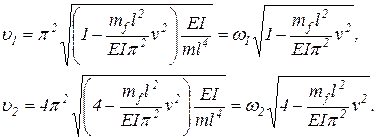
| (47) |
Если скорость транспортируемого потока v = 0, то первая частота собственных колебаний будет определяться по выражению
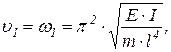
|
совпадающему с (32).
Из анализа приведенных формул можно сделать некоторые выводы относительно влияния скорости потока на вибрацию трубы. Учет скорости потока снижает значение собственной частоты, хотя степень ее влияния зависит от конкретных условий эксплуатации. При достаточно высокой скорости транспортируемого потока собственная частота может оказаться равной нулю. Этому условию соответствует значение первой критической скорости
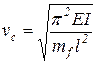
| (48) |
при которой инерционная сила потока, возникающего вследствие кривизны траектории потока, находится в равновесии с восстанавливающей силой, связанной с упругостью трубы. При скорости движения выше критической, силы инерции превосходит восстанавливающую силу и трубопровод теряет устойчивость.
Полученный результат (возможность потери трубопроводом устойчивости) обусловлен именно наличием в уравнении (44) слагаемого, содержащего первую производную по времени и отличающегося от слагаемого, также содержащего первую производную по времени, в уравнении (40). Если бы в уравнении (44) не было данного слагаемого, то частоты собственных колебаний отличались бы от значений, определяемых по выражению (39), лишь численным значением коэффициента r.
В табл. 7 приведены значения первой критической скорости vc потока для данных примера, рассмотренного в параграфе 2.3, и расширенных еще двумя значениями плотности потока и одним вариантом трубопровода.
Таблица 7
Значения критической скорости транспортируемого потока vc, м/с
| ÆDxh | p=50 | p2=200 | p3=500 | p4=650 | p5=850 | p6=1000 |
| 1420x16,5 | 878,5 | 439,3 | 277,8 | 243,7 | 313,1 | 196,4 |
| 1220x12 | 694,4 | 347,2 | 219,6 | 192,6 | 168,4 | 155,3 |
| 1020x14 | 686,5 | 343,2 | 217,1 | 190,4 | 166,5 | 153,5 |
| 1020x10 | 578,8 | 289,4 | 183,0 | 160,5 | 140,4 | 129,4 |
| 720x11,3 | 518,7 | 259,4 | 164,0 | 143,9 | 125,8 | 116,0 |
Как следует из таблицы, значение критической скорости более чем на порядок превышает возможные скорости потока. Определим длину пролета трубопровода, при которой сила Кориолиса начала бы превосходить восстанавливающую силу трубопровода.
Формулу (49) можно переписать в следующем виде:
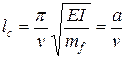 , ,
| (48) |
где 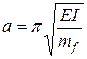 .
.
В табл. 8 приведены значения параметра.
Таблица 8
Значения параметра а
| ÆDxh | p1=50 | р2=200 | р3=500 | р4=650 | р5=850 | р6=1000 |
| 1420x16,5 | 22,0×103 | 11,0×103 | 6,9×103 | 6,1×103 | 5,З×103 | 4,9×103 |
| 1220x12 | 17,4×103 | 8,7×103 | 5,5×103 | 4,8×103 | 4,2×103 | 3,9×103 |
| 1020x14 | 17,2×103 | 8,6×103 | 5,4×103 | 4,8×103 | 4,2×103 | 3,8×103 |
| 1020x10 | 14,5×103 | 7,2×103 | 4,6×103 | 4,0×103 | 3,5×103 | 3,2×103 |
| 720x11,3 | 13,0×103 | 6,5×103 | 4,1×103 | 3,6×103 | 3,1×103 | 2,9×103 |
Полученные с учетом значений параметра а величины расстояний между опорами намного превышают существующие на практике. Но такая длина пролета трубопровода может получиться, например, в результате просадки нескольких соседних опор (ситуация, имевшая место на практике и приведшая к аварии нефтепровода надземной прокладки). В то же время, если длина пролета трубопроводной системы (только для рассмотренного примера) меньше соответствующих табл. 8, то сила Кориолиса не может быть причиной потери трубопроводом устойчивости.
Возможность апериодического движения в механических системах, описываемых уравнениями (42) и (43), связана с появлением в этих уравнениях слагаемых, содержащих первую производную по времени t. Наличие разности в подкоренных выражениях в формулах (43) и (47) приводит к возможности появления под знаком квадратного корня отрицательного числа. Это значит, что собственная частота механической системы может быть комплексным числом, то есть
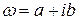 , ,
|
где 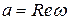 ,
, 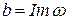 .
.
Тогда решение (45) уравнения (44) примет вид
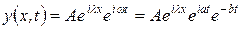 . .
|
Отсюда следует, что условие
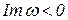
соответствует неограниченному росту перемещений точек механической системы с течением времени, условие
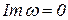
соответствует гармоническим колебаниям трубопровода с постоянной амплитудой, условие
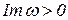
соответствует затухающим с течением времени гармоническим колебаниям. Полученный результат точно соответствует общему динамическому (в отличие от статического или бифуркационного) критерию устойчивости деформируемых тел
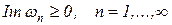 . .
| (49) |
Согласно динамическому критерию устойчивости состояние равновесия считается устойчивым, если возмущения со временем затухают (при t®¥). Условно при этом также считают состояние равновесия устойчивым, если для возмущений получают только периодические по времени решения. При динамическом критерии устойчивости состояние равновесия считается неустойчивым, если возмущения неограниченно возрастают при t®¥.
Как показано в последнем примере, собственная частота 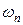 является функцией в том числе и параметров транспортируемого по трубопроводу потока, дополнительно нагружающего трубопровод. Поэтому необходимо отметить, что условие (51) определяет область устойчивости в пространстве параметров нагружения, характеризующих рассматриваемую конкретную задачу, так как собственные значения
является функцией в том числе и параметров транспортируемого по трубопроводу потока, дополнительно нагружающего трубопровод. Поэтому необходимо отметить, что условие (51) определяет область устойчивости в пространстве параметров нагружения, характеризующих рассматриваемую конкретную задачу, так как собственные значения 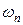 (наряду с зависимостью от формы механической системы и структуры соотношений упругости) также зависят от параметров нагружения (величин, характеризующих нагрузки).
(наряду с зависимостью от формы механической системы и структуры соотношений упругости) также зависят от параметров нагружения (величин, характеризующих нагрузки).
Выводы
При использовании вибрационной диагностики для оценки технического состояния механической системы одной из численных характеристик, количественно отражающих это состояние, является собственная частота (спектр собственных частот) механической системы.
В общем случае собственная частота механической системы является функцией:
· геометрических размеров механической системы (например, D, h и l);
· механических характеристик системы (например, Е и rр );
· условий закрепления (r);
· характеристик технологического процесса (например, rf и v).
При этом приведенные в качестве примеров количественные характеристики ни в коем случае не ограничивают возможные аргументы собственной частоты реальной механической системы.
Значение собственной частоты механической системы в общем случае является функцией выбранной расчетной схемы, то есть набора учитываемых в расчете силовых факторов, математической модели рассматриваемой системы и принятых граничных условий.
Как показано выше, изменение жесткости или массы механической системы за счет износа, ошибки при определении численных характеристик системы или ошибки выбора расчетной схемы (выбора набора учитываемых в расчете силовых факторов) могут привести к отличию между расчетной и действительной собственными частотами.
Одной из возможных причин потери трубопроводом устойчивости, сопровождаемой неограниченным ростом перемещений, является сила инерции транспортируемого потока, связанная с кориолисовым ускорением (сила Кориолиса).
Динамическим критерием устойчивости состояния равновесия механических систем является условие 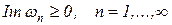 .
.
Таким образом, собственная частота является численной характеристикой механической системы и ее значение может принципиально изменяться в зависимости от износа и учета различных силовых факторов.
Дата добавления: 2018-09-24; просмотров: 925;
