Вибрация многомассовой механической системы под действием внешней нагрузки
В предыдущем параграфе была рассмотрена одномассовая система (система с одной степенью свободы). Реальные технические конструкции представляют собой сложные системы с большим числом степеней свободы и, поэтому, описываются многомассовыми системами, системами с распределенными параметрами или их сочетанием. При решении уравнения движения системы с распределенными параметрами численным методом (часто единственный возможный метод решения для сложных систем) совершается переход от системы с непрерывно распредленными параметрами к некой эквивалентной системе с дискретным распределением параметров. Этот переход с механической точки зрения означает замену рассматриваемой реальной системы с распределенными параметрами некой эквивалентной многомассовой системой. Поэтому многомассовая система является, возможно, наиболее часто используемой математической моделью, идеализирующей реальную систему.
Рассмотрим многомассовую (число дискретных масс больше единицы) систему. Математически анализ многомассовой механической системы осложняется необходимостью решения большого числа составляющих систему уравнений движения. Для таких систем уравнений эффективным средством упрощения записи является матричный метод, при котором большие системы уравнений записываются с помощью краткой системы обозначений - в матричной форме.
Рассмотрим уравнение движение системы без демпфирования, показанной на рис.10. Система состоит из двух масс m1 и m2, трех пружин с жесткостью k1, k2 и k3 и нагружена внешними возмущающими нагрузками F1 и F2 приложенными соответственно к массам m1 и m2.
Система уравнения движения такой системы имеет вид
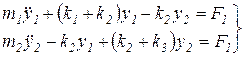 , ,
| (60) |
Систему уравнений (60) можно переписать в матричной форме
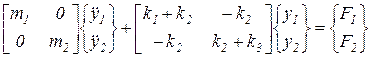 . .
| (61) |
Решение уравнений (60) или (61), как и любого неоднородного, является суммой двух слагаемых: общего решения однородного уравнения (без правой части) и частного решения неоднородного уравнения (с правой частью).
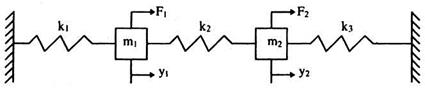
Рис.10. Двухмассовая система (система с двумя степенями свободы).
Уравнение свободных колебаний рассматриваемой системы в матричной форме имеет вид
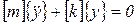 . .
| (62) |
где 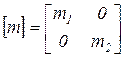 - матрица масс системы;
- матрица масс системы;
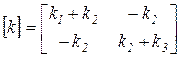 - матрица жесткости системы;
- матрица жесткости системы;
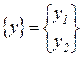 ,
, 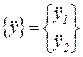 - соответственно векторы перемещений и ускорений.
- соответственно векторы перемещений и ускорений.
Для гармонического движения выполняется условие
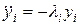 , (i=1,2) , (i=1,2)
| (62) |
где 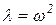 .
.
Тогда уравнение (62) примет вид
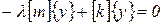 . .
| (62) |
или
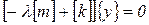 . .
| (63) |
Умножая слева уравнение (63) на матрицу 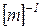 и производя перестановку, получим
и производя перестановку, получим
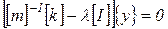 , ,
| (64) |
где 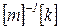 ‑ динамическая матрица системы;
‑ динамическая матрица системы;
 ‑ единичная матрица.
‑ единичная матрица.
Выражение (64) представляет собой систему однородных алгебраических уравнений относительно переменных уi. Для существования не равного тождественно нулю решения необходимо и достаточно, чтобы определитель, составленный из коэффициентов уравнения (64), был равен нулю. Следовательно, получаем уравнение
 , ,
| (65) |
которое называется характеристическим уравнением системы. В общем случае для системы с n степенями свободы уравнение (65) представляет собой полином по 1 вида
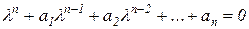 . .
| (66) |
Корни характеристического уравнения li, называются собственными значениями, а собственные частоты рассматриваемой механической системы без демпфирования определяются из выражения
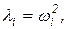 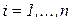 . .
| (67) |
Подставляя li в матричное уравнение (64), получим соответствующую (или главную) форму колебаний 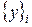 , которая также называется собственным вектором. Собственный вектор представляет собой схему деформации конструкции на соответствующей собственной частоте. Поскольку уравнение (64) однородное, то существует неединственное решение для собственного вектора, а можно получить только их отношение. Таким образом, собственная форма определяется отношением амплитуд движения в различных точках конструкции при возбуждении ее на собственных частотах. С другой стороны, действительная амплитуда зависит от начальных условий, а также от системы приложения и амплитуды внешней возмущающей нагрузки.
, которая также называется собственным вектором. Собственный вектор представляет собой схему деформации конструкции на соответствующей собственной частоте. Поскольку уравнение (64) однородное, то существует неединственное решение для собственного вектора, а можно получить только их отношение. Таким образом, собственная форма определяется отношением амплитуд движения в различных точках конструкции при возбуждении ее на собственных частотах. С другой стороны, действительная амплитуда зависит от начальных условий, а также от системы приложения и амплитуды внешней возмущающей нагрузки.
Рассмотрим пример расчета двухмассовой системы, показанной на рис. 11, для которой:
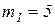 кг,
кг, 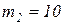 кг, k1=k2= 2 Н/м; k3= 4 Н/м.
кг, k1=k2= 2 Н/м; k3= 4 Н/м.
Подставляя эти значения в уравнение (62), получим
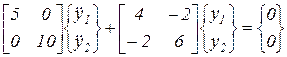 . .
|
Таким образом, уравнение (64) приводится к виду
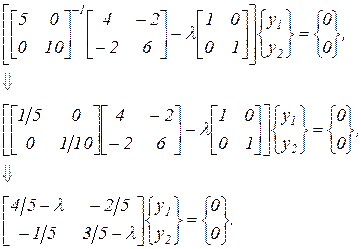 . .
|
Для ненулевого решения определитель должен быть равен нулю, следовательно
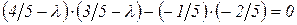 .
.
Тогда
 ‑ характеристическое уравнение.
‑ характеристическое уравнение.
Корнями характеристического уравнения являются
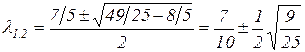 .
.
Таким образом, l1=2/5 и l2=1, а собственные частоты
 и
и 
Подставляя l1 и l2 обратно в матричное уравнение, получим две собственные формы. Так, для l1
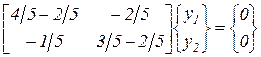 ,
,
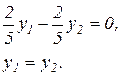
Таким образом, собственная форма для собственной частоты w1, имеет вид
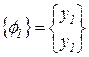 ,
,
где значение у1, произвольно. Аналогично получается собственная форма для l2
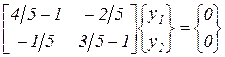 ,
,
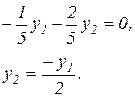
Таким образом, собственная форма для собственной частоты w2 имеет вид
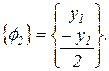
Для произвольного отклонения у1 = 1 две собственные формы имеют вид:
 для
для 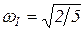 ;
;
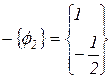 для
для  .
.
В результате установили, что рассмотренная система совершает гармоническое движение, которое начинается на одной из двух возможных частот, как показано на рис. 11. Как видно из рисунка, массы движутся либо в фазе, либо со сдвигом на 180° одна относительно другой. Поскольку массы достигают максимальных перемещений одновременно, то можно определить узловые точки
.
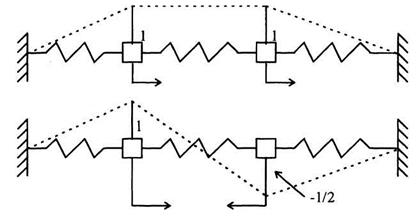
Рис. 11.Собственные формы колебаний двухмассовой системы:
(а) первая форма вибрации:  ;
;
(б) вторая форма вибрации: 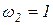 .
.
Итак, решение уравнения (63) приводит к n собственным значениям и соответствующим им n собственным векторам. Это значит, что определенные собственное значение 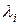 и собственный вектор
и собственный вектор 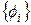 будут удовлетворять уравнению (63), то есть
будут удовлетворять уравнению (63), то есть
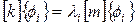 . .
| (68) |
Умножая слева уравнение (68) на транспонированный вектор другой собственной формы i, получим
 . .
| (69) |
Теперь запишем уравнение для j-й собственной формы и умножим его слева на транспонированный вектор i-й собственной формы
 . .
| (70) |
Так как [m] и [k] - симметричные матрицы, то
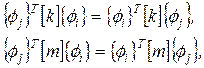 . .
| (71) |
Поэтому, вычитая уравнение (70) из уравнения (69), получим
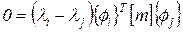 . .
| (72) |
Если 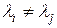 (рассматриваем две различные собственные частоты), то
(рассматриваем две различные собственные частоты), то
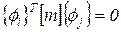 . .
| (73) |
а из уравнения (70) видно, что
 . .
| (74) |
Равенства (73) и (74) определяют свойства ортогональности собственных форм вибрации по отношению к матрицам масс и жесткости механической системы соответственно.
Из уравнения (72) следует, что если i = j, то две собственные формы не являются обязательно ортогональными. Тогда уравнение (73) равно некоторой скалярной величине, отличной от нуля, например Мi, то есть
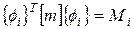 , i = 1,2,3,…n. , i = 1,2,3,…n.
| (75) |
Из уравнения (70) следует, что
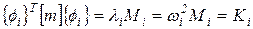 , i = 1,2,3,…n. , i = 1,2,3,…n.
| (76) |
где Мi и Кi называются соответственно обобщенной массой и обобщенной жесткостью системы.
Для определения обобщенной массы и обобщенной жесткости используем численные значения собственных форм, вычисленные выше. Подставляя  в выражение (75), получим обобщенную массу М1 для первой формы
в выражение (75), получим обобщенную массу М1 для первой формы

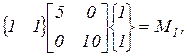
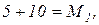
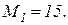
Аналогично, подставляя  в выражение (76), получим
в выражение (76), получим
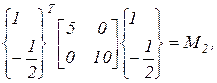

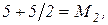

В результате получили, что обобщенные массы М1 и М2 для первой и второй собственных форм вибрации соответственно равны 15 и 15/2. Обобщенные жесткости К1 и К2 для первой и второй собственных форм определяются по выражениям
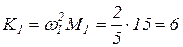 и
и 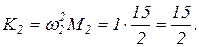
Рассмотрим вынужденные колебания данной двухмассовой механической системы. Уравнение (61) можно представить в виде
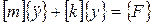 , ,
| (77) |
где 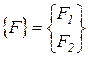 ‑ вектор внешней возмущающей нагрузки.
‑ вектор внешней возмущающей нагрузки.
Воспользуемся свойствами ортогональности собственных форм, рассмотренных выше. Из условия (75) и (76) следует, что если матрицу масс или жесткости умножить справа и слева соответственно на вектор собственной формы и на его транспонированный вектор, то в результате получим некоторую скалярную величину. Таким образом, используя матрицу 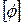 , столбцами которой являются векторы собственных форм, получаем некоторое преобразование координат. Координаты у преобразуются в координаты h с помощью выражения
, столбцами которой являются векторы собственных форм, получаем некоторое преобразование координат. Координаты у преобразуются в координаты h с помощью выражения
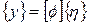 , ,
| (78) |
где
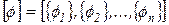 . .
| (79) |
Подставив выражение (78) в (77), получим
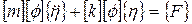 , ,
| (80) |
Умножая слева уравнение (80) на 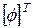 , получим
, получим
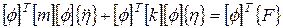 , ,
| (81) |
В уравнении (81) матрицы масс и жесткости умножаются справа и слева соответственно на векторы и транспонированные векторы всех собственных форм в отличие, например, от выражений (75) и (76). Таким образом, произведение представляет собой матрицы [М] и [К], у которых диагональные элементы являются некоторыми постоянными величинами, а все недиагональные элементы равны нулю, то есть
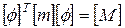
| (82) |
и
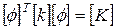 , ,
| (83) |
где [М] и [К] являются диагональными матрицами. Отсюда уравнение (81) можно записать в виде
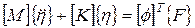 , ,
| (84) |
Уравнение (84) представляет собой систему n уравнений вида
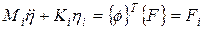 , ,
| (85) |
где 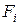 ‑ i-й столбец матрицы, то есть n-я собственная форма;
‑ i-й столбец матрицы, то есть n-я собственная форма;
Мi ‑ i-я обобщенная масса;
Кi ‑ i-я обобщенная жесткость.
Уравнение (85) является уравнением движения для системы с одной степенью свободы, показанной на рис.12. И в данном случае раскрывается физический смысл понятий обобщенная масса и обобщенная жесткость.
Использование обобщенных масс жесткости позволяет описать движение каждой массы многомассовой механической системы уравнением движения одномассовой системы. Следовательно, выводы, полученные в предыдущем параграфе для одномассовой системы, верны и для движения каждой массы многомассовой механической системы, а следовательно, и всей многомассовой системы в целом. Но многомассовая механическая система имеет и принципиальное отличие от одномассовой системы, состоящее, в частности, в более сложном выражении собственных форм.
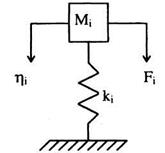
Рис. 12. Система с одной степенью свободы
С учетом выражения (76) уравнение (85) можно записать в более простом виде
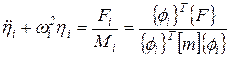 . .
| (86) |
После того, как получено решение уравнения (84) для всех значений h, решение для исходных координату определяется обратным преобразованием из выражения (78).
Рассмотрим численный пример для системы, показанной на рис.10. Матричное уравнение имеет вид
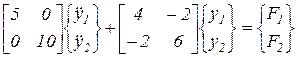 .
.
Собственными частотами и собственными формами вибрации являлись
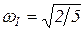 ,
, 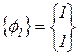 ;
;
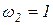 ,
, 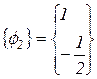 ;
;
Следовательно, матрица 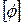 , полученная с использованием собственных форм, имеет вид
, полученная с использованием собственных форм, имеет вид
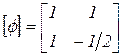 .
.
Координаты у преобразуются с помощью выражения
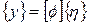 .
.
Тогда
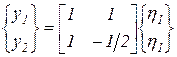 .
.
Сделаем замену переменных в матричном уравнении и умножим его слева на 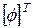 . В результате получим
. В результате получим
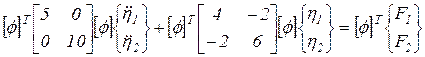 .
.
Проведя промежуточные вычисления, получим
 .
.
Следовательно, уравнения движения в координатах h имеют вид
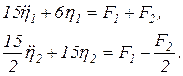
Обобщенные массы и жесткости для двух собственных форм, как видно, совпадают с ранее вычисленными. Таким образом, система с двумя степенями свободы распадается на две системы с одной степенью свободы, показанные на рис.13.
После того как определили временные характеристики в координатах h1, и h2, определим их в исходной системе координату. Получаем
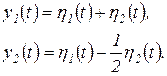
Последняя система уравнений фактически постулирует очень важный принцип механических колебаний, который состоит в том, что любое свободное колебательное движение можно представить в виде суммы колебаний на каждой из главных частот в некотором соотношении и с относительной фазой. В общем случае для системы с n степенями свободы
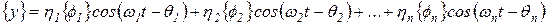 .
.
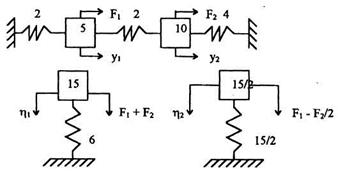
Рис. 13. Система с двумя степенями свободы без демпфирования, распавшаяся на две системы с одной степенью свободы
Для рассмотренной выше двухмассовой системы при произвольных начальных условиях результирующее колебательное движение представляется суммой двух главных форм вибрации.
Дата добавления: 2018-09-24; просмотров: 704;
