Пример расчета собственных частот
На простом примере рассмотрим как изменяется значение собственной частоты при изменении характеристик самой системы.
Как следует из (32), собственная частота является функцией жесткости системы EI, массы m, геометрических размеров (длины l) и условий закрепления. Поэтому в качестве примера рассмотрим труб провод-балку длиной 25 м, идеально шарнирно опертый в обеих точках опоры.
Рассмотрим четыре варианта трубопровода со следующими геометрическими размерами: Æ1420x16,5 мм, Æ1220x12 мм, Æ1020x14 мм и Æ1020x10 мм. Каждый из этих трубопроводов может транспортировать поток со следующими значениями плотности: 50 кг/м3,200 кг/ м3, 500 кг/ м3 и 650 кг/ м3.
Согласно СНиП 2.05.06-85 Е = 206000 МПа или 206000х106 Па.
Используем только номинальные значения геометрических параметров и механических характеристик материала трубы, норматива установленные СНиП, и не учитываем возможность их отклонения с номинального значения. Считаем также поперечное сечение труб полым идеальным кольцом и не учитываем возможную овальность поперечного сечения.
Момент инерции поперечного сечения трубы
,
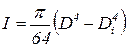где D - внешний диаметр трубы;
Di - внутренний диаметр трубы, Di = D - 2h (h - толщина стенки трубы).
В рассматриваемом случае значения внутреннего диаметра трубопровода будут соответственно равны 1387 мм, 1196 мм, 992 мм 1000 мм.
Определим момент инерции и жесткость поперечного сечения для труб различного диаметра
труба Æ1420x16,5 мм -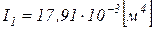 
, 
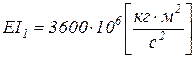
труба Æ1220x12 мм -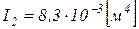 
, 
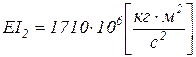
труба Æ1020x14 мм -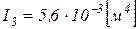 
, 
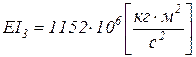
труба Æ1020x10 мм -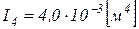 
, 
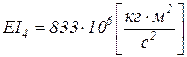
Суммарная масса единицы длины трубопровода определяется из условия
,
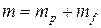где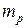 
- масса единицы длины трубы, [кг/м];
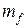- масса транспортируемого потока в единице длины трубопровода, [кг/м].
Масса единицы длины трубы
,
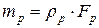где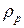 
- плотность материала стенки трубы, р = 7850 [кг/м3];
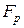- площадь кольца трубы,
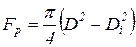
В рассматриваемом случае площадь кольца трубы соответственно равна72,7×10-3 м2, 45,5×10-3 м2, 44,2×10-3 м2 и 31,7×10-3 м2. Тогда масса единицы длины трубы mp соответственно равна 570,7 [кг/м], 357,2 [кг/м], 347,0 [кг/м] и 249,0 [кг/м].
Масса транспортируемой среды в единице длины трубопровода
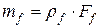
где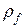 
- плотность транспортируемого потока;
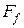- площадь внутреннего сечения трубы,
.
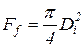Для рассматриваемых трубопроводов площадь внутреннего сечения соответственно равна 1,51 м2, 1,12 м2, 0,772 м2 и 0,785 м2. Тогда масса потока на единицу длины трубопровода зависит от двух аргументов - плотности потока и геометрических размеров трубы. Поэтому значения в зависимости от этих величин удобно привести виде табл. 1.
Таблица 1
Значения массы потока 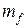на единицу длины трубопровода
| ÆDxh | р1 = 50 | р2 = 200 | р3 = 500 | р4 = 650 |
| 1420x16,5 | 75,5 | 302,0 | 755,0 | 981,5 |
| 1220x12 | 56,0 | 224,0 | 560,0 | 728,0 |
| 1020x14 | 38,6 | 154,4 | 386,0 | 501,8 |
| 1020x10 | 39,25 | 392,5 | 510,3 |
Значения массы единицы длины трубопровода т приведены табл.2.
Таблица 2
Значения суммарной массы единицы длины трубопровода m
| ÆDxh | р1 = 50 | р2 = 200 | р3 = 500 | р4 = 650 |
| 1420x16,5 | 646,2 | 872,7 | 1325,7 | 1552,2 |
| 1220x12 | 413,2 | 581,2 | 917,2 | 1085,2 |
| 1020x14 | 385,6 | 501,4 | 733,0 | 848,8 |
| 1020x10 | 288,25 | 406,0 | 641,5 | 759,3 |
Полученные значения массы единицы длины трубопровода позволяют вычислить значения радикала в формуле (32), которые приведены в табл. 3.
Таблица 3
Значения радикала в формуле (32)
| ÆDxh | р1 = 50 | р2 = 200 | р3 = 500 | р4 = 650 |
| 1420x16,5 | 3,82 | 3,29 | 2,67 | 2,47 |
| 1220x12 | 3,25 | 2,74 | 2,18 | 2,01 |
| 1020x10 | 2,77 | 2,43 | 2,01 | 1,86 |
| 1020x10 | 2,72 | , 2,29 | 1,82 | 1,68 |
Значение частоты зависит от формы вибрации. Рассчитаем значение частоты для первых двух форм вибрации. В табл. 4 приведены значения собственной частоты для первой формы вибрации трубопровода-балки.
Таблица 4
Значения собственных частот трубопровода при первой форме вибрации
| ÆDxh | р1 = 50 | р2 = 200 | р3 = 500 | р4 = 650 |
| 1420x16,5 | 37,7 | 32,5 | 26,3 | 24,35 |
| 1220x12 | 32,1 | 27,1 | 21,6 | 19,82 |
| 1020x10 | 27,3 | 23,9 | 19,8 | 18,4 |
| 1020x10 | 26,8 | 22,6 | 18,0 | 16,5 |
В табл. 5 приведены значения собственной частоты для второй формы вибрации трубопрвода-балки.
Таблица 5
Значения собственных частот трубопровода при второй форме вибрации
| ÆDxh | р1 = 50 | р2 = 200 | р3 = 500 | р4 = 650 |
| 1420x16,5 | 150,8 | 129,9 | 105,4 | 97,5 |
| 1220x12 | 128,3 | 108,2 | 86,2 | 79,3 |
| 1020x10 | 109,2 | 95,7 | 79,2 | 73,6 |
| 1020x10 | 107,2 | 90,5 | 72,0 | 66,2 |
На рис.8 и 9 показано изменение частоты собственных колебаний трубопровода-балки в зависимости от изменения жесткости поперечного сечения трубы и плотности транспортируемого потока для первой и второй форм вибрации.
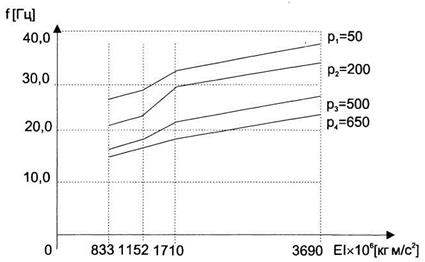
Рис.8. Значения собственных частот при первой форме вибрации
Согласно полученным результатам изменение поперечного сечения трубы за счет изменения ее геометрических размеров (внешнего диаметра и толщины стенки трубы) и изменение плотности транспортируемого продукта приводят к принципиальному изменению значения частоты собственных колебаний. При этом скорость изменения частоты собственных колебаний при изменении геометрических размеров явно выше, чем при изменении плотности транспортируемого продукта.
Следует обратить внимание еще на одно обстоятельство. Изменение системы в рассмотренных примерах приводило к принципиальному изменению значения частоты собственных колебаний, но движение механической системы остается гармоническим, то есть амплитуда изменялась, но система (трубопровод) сохраняла устойчивость. Но одним из главных вопросов технической диагностики является именно вопрос о том, когда или при каких условиях механическая система потеряет устойчивость. В рамках рассмотренной в параграфе 2.2 расчетной схемы потеря устойчивости невозможна. Поэтому рассмотрим задачу в другой более сложной постановке (рассмотрим большее количество силовых факторов).
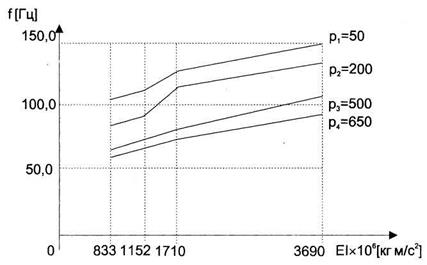
Рис.9. Значения собственных частот по второй форме вибрации
Дата добавления: 2018-09-24; просмотров: 1358;