Качественные характеристики САУ
4.3.1.Временные характеристики
Основными задачами, которые решаются при анализе систем управления является выявление и количественная оценка свойств поведения САУ. Эти задачи часто решаются через характеристики элементов автоматики и способов их взаимосоединения. Решение задач анализа САУ предполагает выбор элементов автоматики и их взаимосвязь, обеспечивающую требуемые характеристики системы. Анализ и синтез систем управления сводится в общем случае к решению следующих 3-х задач:
· в нахождении качественных характеристик САУ;
· определение условий устойчивости, при которых система возвращается к заданному состоянию плавно или через колебания уменьшающейся амплитуды;
· выявление и устранение ошибок в установившемся режиме работы САУ.
Выше были приведены некоторые показатели качества САУ в динамическом режиме. Было отмечено, что для оценки переходного процесса применяется скачкообразное изменение входного сигнала. Реакция системы на единичный скачок называют переходной функцией. Пусть функция единичного скачка (ступенчатая функция) входного сигнала имеет вид
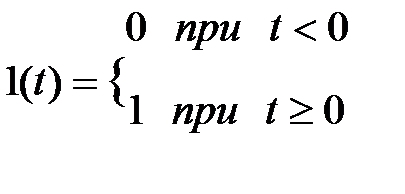 . (4.1)
. (4.1)
График единичной ступенчатой функции представлен на рис.4.3.
Рис. 4.3. Единичная ступенчатая функция
Используя преобразование Лапласа (3.1), связь между выходным сигналом (реакцией системы) и входным единичным скачком (4.1) запишем в виде
H(s) = W(s) U(s). (4.2)
Воспользовавшись таблицей преобразований Лапласа, получим U(s)=1/s.
Тогда изображение H(s) переходной функции h(t) определяется из (4.2)
H(s)=W(s)/s. (4.3)
Для любого входного воздействия, комплексная передаточная функция может быть определена из правой части равенства (3.1), тогда
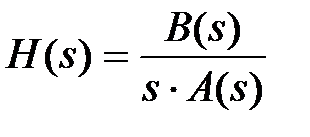 . (4.4)
. (4.4)
Следовательно, изображение переходной функции заданной САУ может быть использована для определения реакции системы на любой сигнал. Действительно подставив в (3.1) выражение для W(s)из(4.3) получим
Y(s) = sH(s)U(s) (4.5)
Переходная функция H(s) в комплексной форме является одной из временных характеристик САУ и представляет один из операторов преобразования входной функции в выходную. Изменением функции H(s) можно получить систему с заданным поведением при управлении.
4.3.2. Частотные характеристики
Наряду с временными характеристиками, для качественного анализа системы используются частотные характеристики. В данном случае на линейную систему оказывается гармоническое входное воздействие
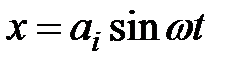 (4.6)
(4.6)
с амплитудой ai и частотой w, изменяющейся в произвольном диапазоне.
В линейных САУ установившаяся реакция будет изменяться по гармонической зависимости.
Для анализа САУ с помощью частотных характеристик используется прямое преобразование Фурье дифференциальных уравнений системы (2.1)
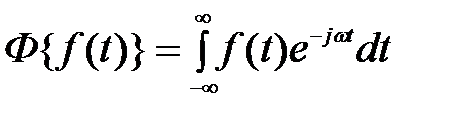 .
.
Так же для частотного преобразования можно использовать двухстороннее преобразование Лапласа, формально заменив s на jw.
Частотную передаточную функциюможно получитьпросто, заменив s на jw в выражении для комплексной ПФ W(s) (3.1), тогда .
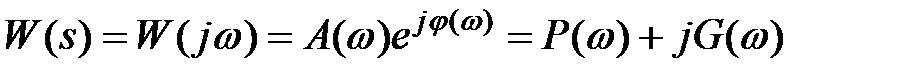 . (4.7)
. (4.7)
Здесь A(w), j(w) называются соответственно амплитудно-частотной и фазо-частотной характеристикой системы. P(w) ,G(w) – вещественная и мнимая частотные характеристики. Годограф функции W(jw) представляет амплитудно-фазо-частотную характеристику (АФЧХ).
Амплитудно-частотная характеристика (АЧХ) определяется из выражения
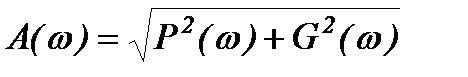 . (4.8)
. (4.8)
Фазо-частотная характеристика (ФЧХ) определяется как
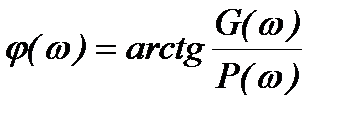 (4.9)
(4.9)
Таким образом, модуль 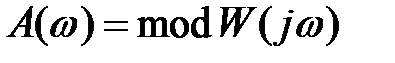 (4.8) является амплитудно- частотной функцией, её график – амплитудно-частотной характеристикой.
(4.8) является амплитудно- частотной функцией, её график – амплитудно-частотной характеристикой.
Аргумент 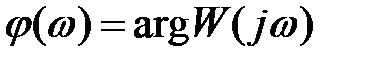 (4.9) называется фазо-частотной функцией, его график – фазо-частотной характеристикой.
(4.9) называется фазо-частотной функцией, его график – фазо-частотной характеристикой.
При гармоническом воздействии в устойчивых системах, после окончания переходного процесса, выходная величина также изменяется по гармоническому закону, но с другими амплитудой и фазой. При этом отношение амплитуд выходной и входной величин равно модулю 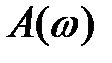 , а сдвиг фазы – аргументу
, а сдвиг фазы – аргументу 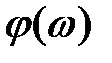 частотной передаточной функции. И, следовательно, амплитудно-частотная характеристика показывает отношение амплитуд, а фазо-частотная характеристика – сдвиг фазы выходной величины относительно входной в зависимости от частоты входного гармонического воздействия.
частотной передаточной функции. И, следовательно, амплитудно-частотная характеристика показывает отношение амплитуд, а фазо-частотная характеристика – сдвиг фазы выходной величины относительно входной в зависимости от частоты входного гармонического воздействия.
Достоинством частотных методов является то, что частотные характеристики могут быть получены экспериментальным путем без проведения сложных аналитических решений.
Теперь обратим внимание на связь между АЧХ И ФЧХ. Х.У. Боде доказано, что для некоторых звеньев, называемых минимально фазовыми, существует однозначная зависимость между функциями 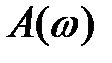 и
и 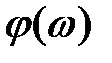 . В общем случае минимально фазовыми называется звено, у которого все полюсы и нули передаточной функции имеют отрицательные или равные нулю действительные части. Минимально-фазовые звенья являются устойчивыми.
. В общем случае минимально фазовыми называется звено, у которого все полюсы и нули передаточной функции имеют отрицательные или равные нулю действительные части. Минимально-фазовые звенья являются устойчивыми.
АЧХ удобно представить в логарифмическом масштабе в децибелах (дБ). При этом логарифмическая амплитудно-частотная характеристика (ЛАЧХ) находится из выражения
L(w)=20 lg A(w). (4.10)
Следует отметить, что Бел представляет логарифмическую единицу, соответствующую десятикратному увеличению мощности.
При графическом построении ЛАЧХ частоты откладываются в логарифмическом масштабе по оси абсцисс в размерности с-1 или в Гц.
Часто результирующая ЛАЧХ может быть приближенно построена в виде так называемой асимптотической ЛАЧХ, представляющей собой совокупность отрезков прямых линий с наклонами, кратными 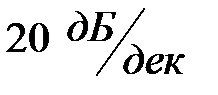 .
.
Дата добавления: 2017-05-18; просмотров: 797;
