Управляемость и наблюдаемость
В п-мерном пространстве состояний 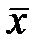 каждому состоянию системы соответствует некоторое положение изображающей точки, определяемое значениями переменные состояния
каждому состоянию системы соответствует некоторое положение изображающей точки, определяемое значениями переменные состояния 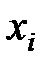 (i = 1, 2,... п).
(i = 1, 2,... п).
Пусть в пространстве состояний 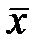 заданы два множества
заданы два множества 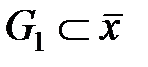 и
и 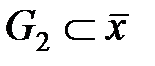 . Рассматриваемая система будет управляемой, если существует управление
. Рассматриваемая система будет управляемой, если существует управление 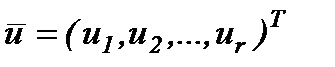 , определенное на конечном интервале времени 0<t<T, переводящее изображающую точку в пространстве
, определенное на конечном интервале времени 0<t<T, переводящее изображающую точку в пространстве 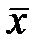 из подобласти G1 в подобласть G2.
из подобласти G1 в подобласть G2.
Система называется наблюдаемой, если в формировании вектора выходных координат 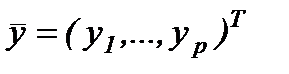 участвуют все составляющие вектора переменных состояния
участвуют все составляющие вектора переменных состояния 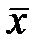 . Если ни одна из составляющих вектора
. Если ни одна из составляющих вектора 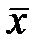 не влияет на формирование выхода системы
не влияет на формирование выхода системы 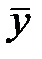 , то такая система будет ненаблюдаемой.
, то такая система будет ненаблюдаемой.
Анализ управляемости и наблюдаемости выполняется с помощью матриц управляемости и наблюдаемости или с помощью грамианов управляемости и наблюдаемости.
Сформируем на основе матриц 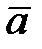 ,
, 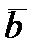 ,
, 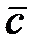 две вспомогательные матрицы
две вспомогательные матрицы
R = [ 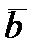 ,
, 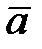
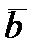 , ...,
, ..., 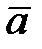 n-1
n-1 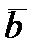 ], D = [
], D = [ 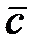 ,
, 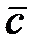
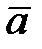 ,…,
,…, 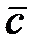
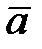 n-1]
n-1]
Mатрицы R и D называются соответственно матрицей управляемости и матрицей наблюдаемости системы. В пакете MATLAB их можно построить с помощью команд ctrbи obsv.
Для того чтобы система (3.2) была управляемой, необходимо и
достаточно, чтобы матрица управляемости имела полный ранг rankR = n.
Для того чтобы система (3.2) была наблюдаемой, необходимо и достаточно, чтобы матрица наблюдаемости имела полный ранг rankD=n.
В случае систем с одним входом и одним выходом матрицы R и D квадратные, поэтому для проверки управляемости и наблюдаемости достаточно вычислить определители матриц R и D. Если они не равны нулю, то матрицы имеют полный ранг.
Дата добавления: 2017-05-18; просмотров: 602;
