Описание системы в переменных состояния

Как указывалось выше САУ, независимо от природы составляющих его звеньев, может быть описана подобными дифференциальными уравнениями (2.1). Эти способы относятся к так называемым внешним описаниям системы. Наоборот, внутреннее описание дается в переменных состояния, предпочтительно используется для тех систем, которые имеют более одного входа и выхода. При этом под переменными состояния системы понимается набор переменных 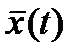, производные первого порядка от которых входят в математическую модель САУ. С другой стороны, под переменными состояния понимается совокупность переменных, значения которых наряду с входным воздействием 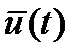позволяет определить будущее состояние системы и выходные величины 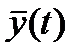. Математическая модель системы в переменных состояния удобна для компьютерного анализа.

Пусть линейная система, характеризуется вектором состояния 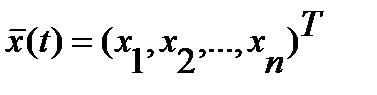, составленным из n-переменных состояния. На вход системы поступают входные управляющие сигналы 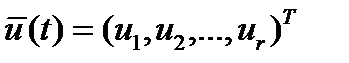. Система описывается следующими уравнениями состояния в векторном виде:

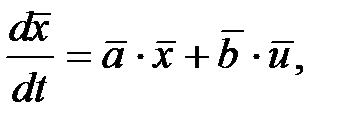(3.2)

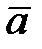где и 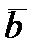- матрицы, составленные из постоянных коэффициентов, имеют вид:

, .

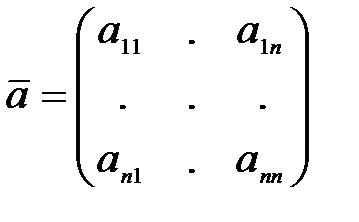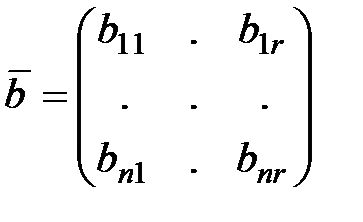Кроме уравнения (3.2) для системы можно составить следующее матричное уравнение:

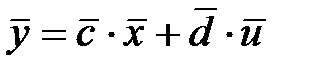(3.3)

Здесь 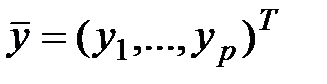-– вектор выходных величин. Матрицы постоянных величин имеют вид

.

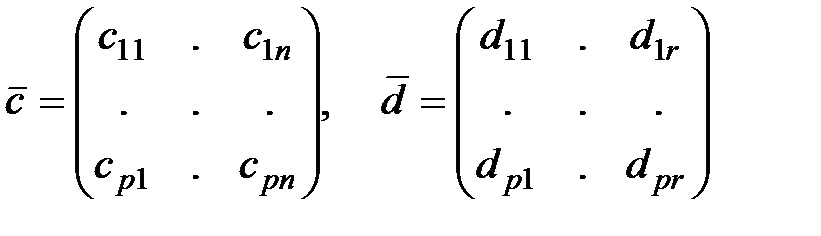Решение систем уравнений (3.2) и (3.3) для некоторого момента времени t = t₀ позволяет найти 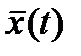для времени t>t₀ , т. е. определить будущее состояние системы, а также дает возможность определить выходные величины .

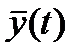Из системы уравнений (3.2) и (3.3) можно исключить вектор 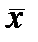. В этом случае преобразование «вход-выход» может быть описан линейными дифференциальными уравнениями n-го порядка с постоянными коэффициентами в виде (2.1).

Все рассматриваемые виды описаний тесно взаимосвязаны, поэтому, зная одно из них, можно получить остальные. Например, связь между матрицами 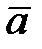, , 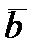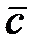описания в пространстве состояний и комплексной передаточной функцией системы W(s) задается уравнением

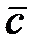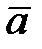W(s)= (sE- )^-1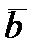

где s  оператор Лапласа, E  единичная матрица.