Математические модели сАУ

В ТАУ для описания и анализа взаимодействия всех элементов между собой удобно использовать математическую модель, которая применима ко всем элементам системы. В связи с этим принято следующее соглашение: каждый элемент САУ рассматривается как устройство – звено системы, в котором происходит преобразование входного воздействия на выходную реакцию т. е. преобразование «вход-выход», характеризующееся оператором преобразования (ОП); взаимодействие между звеньями задается описанием структуры системы. Единообразное описание всех элементов непрерывной системы в виде операторов преобразования может быть осуществлено с помощью дифференциальных уравнений. Дифференциальные уравнения, описывающие динамику любой физической системы, получают на основании фундаментальных физических законов. Этот метод в равной степени применим к механическим, электрическим, гидравлическим, термодинамическим системам.

В программном продукте MATLAB имеются пакеты программ, основанные на аналитических зависимостях, которые позволяют моделировать и исследовать различные САУ. Студентам настоятельно рекомендуется все задачи параллельно решать с применением библиотеки Simulink из MATLAB.

В общем случае для описания «вход-выход» любого элемента и САУ в целом может быть использованы линейные дифференциальные уравнения (ДУ) с постоянными коэффициентами:

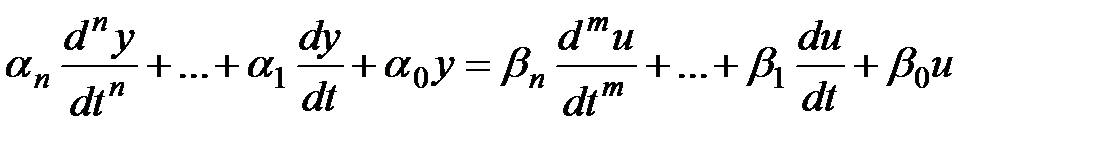. (2.1)

Здесь 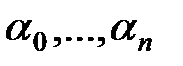, также 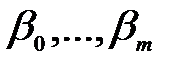– постоянные величины, называемые параметрами звена. Число n называется порядком уравнения. В линейных дифференциальных уравнениях переменные и их производные входят линейно, т. е. в первой степени и без их произведений. Следует отметить, что если на систему действуют несколько входных и выходных воздействий, то для каждой пары входных и выходных воздействий составляется уравнение вида (2.1).

Из теории дифференциальных уравнений известно, что общее решение дифференциального уравнения (2.1) определяется как сумма решений однородного ДУ (без правой части) и частного решения неоднородного ДУ (с правой частью). Искомые n-решения однородного ДУ определяются как 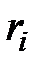(i=1,…,n)…корней характеристического уравнения

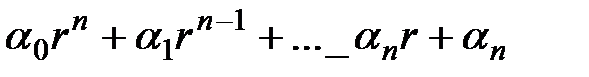=0.

Общее решение однородного ДУ будет

,

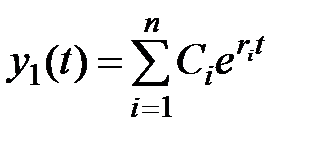где С_i – постоянные интегрирования, определяемые из начальных условий.

Частное решение неоднородного ДУ обычно отыскивается в том виде, в каком дана правая часть уравнения (2.1) и зависит от вида функции u(t) на входе системы.

Введем оператор дифференцирования по времени

.

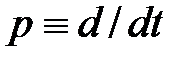Тогда выражение (2.1) запишется в операторной форме

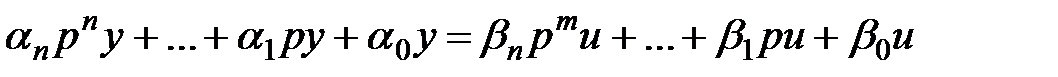
или сокращенно в виде

A(p)y(t) = B(p)u(t), (2.2)

Где 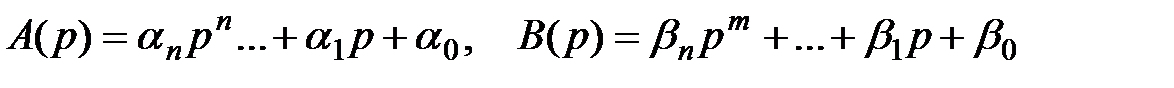– операторные многочлены.

Помимо операторной формы записи в виде (2.2) в качестве математической модели используется операторная передаточная функция. При этом отношение выходной величины к входной величине, называемое операторной передаточной функцией системы определяется из (2.2) как

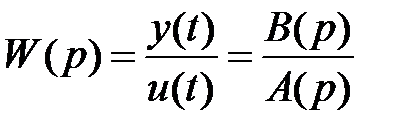(2.3)

Таким образом, чтобы изучить свойство сложной системы и управлять ей необходимо составить математическую модель, чаще в виде дифференциальных уравнений с постоянными коэффициентами.