Преобразование Лапласа, передаточные функции

Наряду с применением дифференциальных уравнений в автоматике для анализа и синтеза САУ используются функции комплексных переменных и преобразование Лапласа. Преобразование Лапласа позволяет решить задачи для САУ путем замены сложных дифференциальных уравнений алгебраическими. Кроме того отпадает необходимость определения постоянных интегрирования и общее решение неоднородного ДУ определяется сразу при любой правой части ДУ (2.1).

Из курса Высшей математики известно, что функция f(t) имеет преобразование Лапласа если выполняется условие Дирихле, т. е. f(t) – непрерывная и дифференцируемая функция, равная нулю при t<0.

Функции f(t) называется оригиналом. Преобразование по Лапласу осуществляется выражением

.

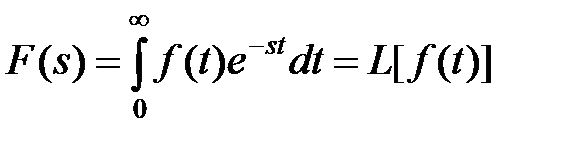Здесь F(s) – изображение функции f(t), 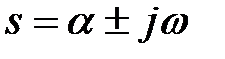- комплексная переменная.

Обратное преобразование Лапласа имеет вид

.

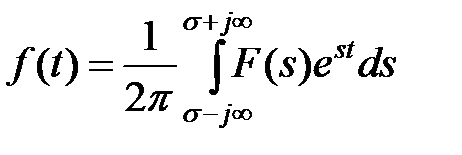Это преобразование позволяет определить оригинал по известному изображению.

На практике для прямого и обратного преобразования по Лапласу обычно пользуются таблицей готовых преобразований.

Оператор преобразования САУ в этом случае определяется в виде комплексной передаточной функции. Комплексная передаточная функция определяется как отношение изображений по Лапласу изображений функций выхода и входа при нулевых начальных условиях, т. е.

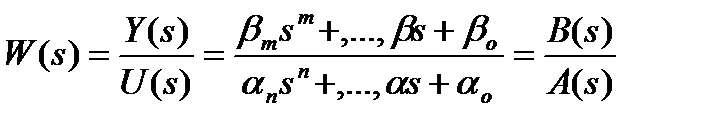. (3.1)

Здесь 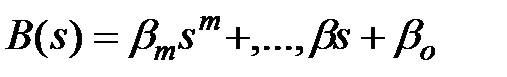, 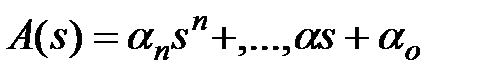– комплексные многочлены, полученные заменой p на s в выражениях для операторных многочленов – В(р) и А(р). Корни характеристического уравнения знаменателя в уравнении z (2.16) называются полюсами. Полюса линейной системы полностью определяют ее устойчивость. Если вещественная часть полюсов отрицательная, то система устойчива. Корни характеристического уравнения числителя в уравнении (2.16) называются нулями.

Нули определяют значение коэффициентов экспоненциальной функции в отклике, но на устойчивость не влияют.