Дифференциальные уравнения объектов с сосредоточенными ёмкостями

Составим дифференциальное уравнение для объекта с сосредоточенными ёмкостями. Уравнения энергетического и материального баланса составляется для каждой ёмкости и представляет собой дифференциальное уравнение первого порядка, если в объекте n ёмкостей, соответственно, будет n уравнений.

Дифференциальное уравнение имеет вид:

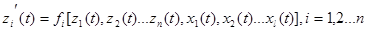; (3-1)

где: z_i – переменные состояния системы, характеризующие содержание вещества или энергии в ёмкостях в каждый момент времени t;

x₁…x_l – внешние (входные) воздействия на систему, приводящие к изменению ее состояния.

В общем случае количество переменных состояния и входных воздействий не равны друг другу.

Обычно требуются не переменные состояния, а некоторые другие величины, связанные с переменными состояния некоторой функциональной зависимостью., эти величины называются выходными величинами системы. Зависимость выходных величин от переменных состояния и входных воздействий выражается в виде:

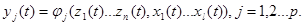; (3-2)

где: y_i – выходные величины системы.

Входные и выходные величины в общем случае не привязаны к входным и выходным потокам вещества или энергии.

Дадим математическое определение динамической системы (такую систему мы в данный момент рассматриваем). Также дадим математическое определение статической системы.

Динамическая система – система, поведение которой описывается дифференциальным уравнением.

Статическая система – система, в дифференциальных уравнениях которой (3-1) производные в левой части равны нулю.

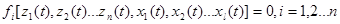(3-3)

Приближенным примером статической системы может служить динамическая система при сравнительно медленном изменении входных воздействий, при этом процесс накопления в ёмкостях вещества или энергии протекает без заметной задержки вслед за изменением входных воздействий.

Система находится в состоянии покоя, если:

- входные воздействия неизменны во времени [ ];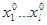

- переменные состояния неизменны во времени [ ].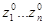

Тогда:

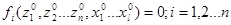. (3-4)

Рассматриваемые нами системы бывают линейными и нелинейными.

Линейной называется система, все функции ХХХ которой в её дифференциальных уравнениях (3-1) линейны. Если хотя бы одна из упомянутых функций нелинейна, то система называется нелинейной.

Нелинейные системы, в свою очередь, делятся на линеаризуемые и нелинеаризуемые. Нелинейная система называется линеаризуемой, если функции ХХХ можно представить в линейном виде. Если хотя бы одну из этих функций в линейном виде представить нельзя, система называется нелинеаризуемой. Линеаризацией называется замена нелинейной функции приближенной линейной функцией.

В общем случае все системы нелинейные, их стремятся линеаризовать. После линеаризации дифференциальные уравнения (3-1) примут вид:

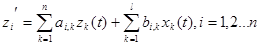(3-5)

Линеаризация всегда сопровождается потерей точности. При линеаризации важно помнить, что устойчивость линеаризованной системы должна отражать устойчивость исходной нелинейной системы.