Спектральное представление сигналов. Преобразование Фурье

Любую функцию времени можно представить в виде суммы соответствующим образом подобранных гармонических колебаний вида:

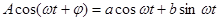(3-29)

где: 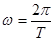- угловая частота колебаний;

Т – период колебаний;

А - амплитуда колебаний;

φ – начальная фаза колебаний.

Графики колебаний показаны на рис. 6-1.

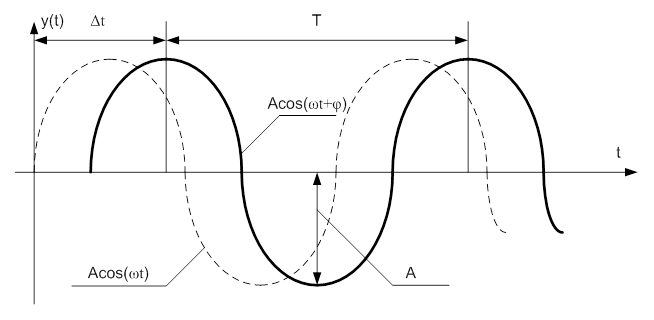
Рис. 3-2. Колебания на входе и на выходе в систему.

Можно записать, что: 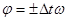, при этом 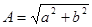и

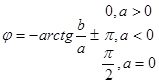(3-30)

Пусть имеется функция произвольного вида x(t), которую нужно представить в виде суммы гармоник. График функции показан на рис. 6-2.

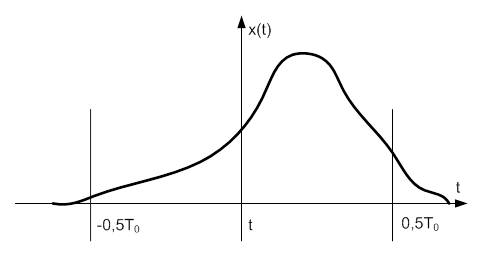
Рис. 3-3. График произвольной функции x(t).

Выберем период Т₀ и построим новую функцию 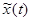, имеющую указанный период и совпадающую с исходной на отрезке 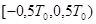. Если функция 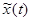удовлетворяет условию 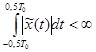, то её можно представить рядом Фурье, то есть суммой гармоник с частотами ω₀, 2ω₀, 3ω₀ (то есть, с частотами, кратными 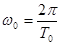). Тогда функция 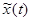будет иметь вид:

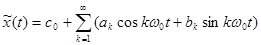. (3-31)

Формула 6-3 представляет собой ряд Фурье, коэффициенты этого ряда определяются формулами:

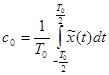, (3-32)

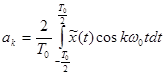, (3-33)

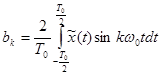. (3-34)

С учетом формул (6-4)-(6-6) ряд Фурье можно записать в виде:

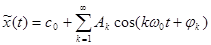. (3-35)

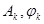- амплитуда и начальная фаза k-ой гармоники.

Совокупность чисел 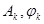называется амплитудным и фазовым спектрами функции 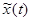, где k – целое положительное число. Разложение функции 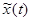в ряд Фурье называется спектральным разложением .

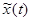С учетом известной формулы Эйлера можно получить

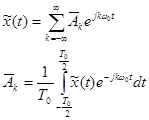; (3-36)

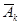- комплексное число, полностью определяющее к-ую гармонику разложения. Связь 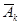с амплитудой и начальной фазой к-ой гармоники определяется формулой:

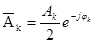. (3-37)

Чтобы получить разложение на гармоники исходной непериодической функции нужно устремить принятый период Т₀ к бесконечности. При этом аплитуды гармоник будут стремиться к нулю (см. формулы 6-7 и 6-8), поэтому необходимо ввести новые комплексные коэффициенты разложения:

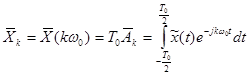. (3-38)

При этом изменится вид (6-7):

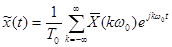. (3-39)

С учетом того, что разность частот соседних гармоник равна ω₀, получим:

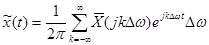. (3-40)

При стремлении Т₀ к бесконечности в итоге получим:

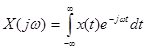(3-41)

Формула (6-12) представляет собой прямое преобразование Фурье. Нижеследующая формула (6-13) представляет собой обратное преобразование Фурье:

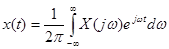. (3-42)

Прямое и обратное преобразования Фурье обозначаются соответственно:

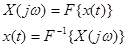. (3-43)

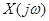- изображение исходной функции по Фурье, комплексная функция частоты. Модуль изображения по Фурье от x(t) является распределением по частотам амплитуд гармоник в разложении x(t). Изображение по Фурье от x(t) называется комплексной спектральной плотностью x(t).