Передаточная функция. Решение дифференциальных уравнений с помощью преобразования Лапласа

Пусть имеется дифференциальное уравнение динамической системы, выведенное на предыдущей лекции:

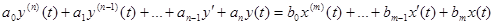. (3-16)

Пусть входное воздействие 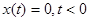, а рассматриваемая система до 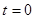находилась в состоянии покоя, то есть, 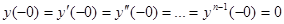. Умножим обе части данного дифференциального уравнения на 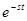и проинтегрируем от -0 до ∞, то есть, выполним преобразование Лапласа. Тогда получим:

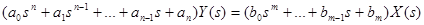(3-17)

Введем обозначения:

,

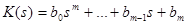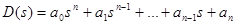. (3-18)

Тогда получим выражение:

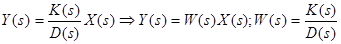, (3-19)

где: W(s) – функция комплексного переменного s, называемая передаточная функция системы (ПФ).

Передаточная функция системы - отношение преобразованной по Лапласу выходной величины системы к преобразованному по Лапласу входному воздействию при нулевых начальных условиях.

Передаточная функция представляет собой описание объекта, подобно дифференциальному уравнению, но при этом она не имеет физического смысла.

Передаточную функцию системы можно получить по ее дифференциальному уравнению, для этого:

1. Производные в левой и правой частях заменить на s в степени, равной порядку заменяемой производной;
2. Полином, полученной в правой части –является числителем передаточной функции, а полином в левой части – ее знаменателем.

Знаменатель передаточной функции является характеристическим уравнением системы (ХУ). Корни ХУ называются полюсами ПФ.

С помощью преобразования Лапласа решить ДУ можно следующим образом:

1. Преобразовать по Лапласу входное воздействие: ;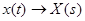

2. По дифференциальному уравнению составить передаточную функцию системы;

3. Записать выражение для изображения выходной величины: ;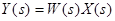

4. Выполнить обратное преобразование Лапласа и получить оригинал выходной величины системы: .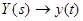

Обратное преобразование Лапласа выполняется по формуле:

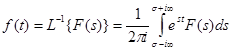; (3-20)

где: σ – действительное число.