Типовые воздействия

Существует несколько видов типовых воздействий.

1. Единичное ступенчатое воздействие (функция Хевисайда);
2. Дельта-функция, функция Дирака;
3. Гармонические колебания единичной амплитуды.

Переходная характеристика – это реакция объекта/системы на функцию Хевисайда.

Импульсная переходная характеристика – реакция объекта/системы на дельта-функцию.

Кривая разгона – реакция объекта/системы на ступенчатое воздействие произвольной величины.

Необходимо иметь в виду следующее. Пусть функция f(t) определена на (-∞,∞), тогда:

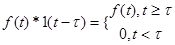; (3-21)

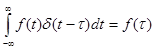. (3-22)

Интеграл свертки

Покажем, что имею любую из описанных динамических характеристик (переходную или импульсную характеристику), можно вычислить реакцию линейной системы на входное воздействие произвольного вида.

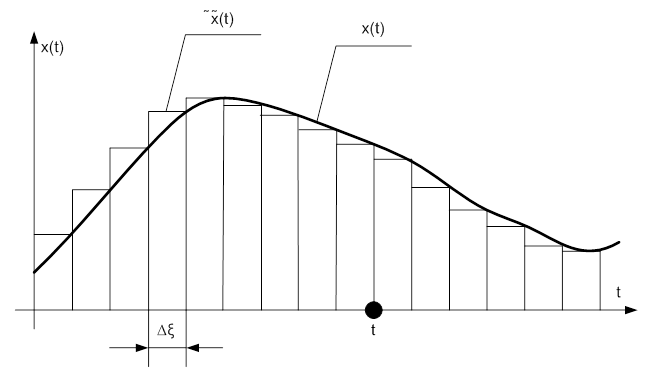
Пусть на входе в динамическую систему имеется произвольное входное воздействие x(t). График зависимости от времени входного воздействия приведен на рис. 5-1.

Рис. 3-1. График зависимости от времени входного воздействия.

Найдем значение выхода системы в произвольный момент времени t (этот момент произволен, но зафиксирован).

Разобьем ось времени на небольшие отрезки длительностью Δξ, далее построим новую функцию времени 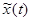, совпадающую с исходной в точках разбиения и остающуюся постоянной в промежутках между ними. Можно записать, что

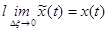. (3-23)

При этом 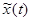- это последовательность прямоугольных импульсов длительностью Δξ, таким образом, реакцию линейной системы на 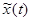можно вычислить как сумму реакций на каждый импульс, взятый отдельно.

Пусть 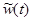- реакция системы на прямоугольный импульс длительностью Δξ и амплитудой 1/Δξ (то есть, на импульс единичной площади). Тогда, если импульсы имеют амплитуду А, то можно записать .

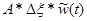Тогда реакция системы (у(t)) в фиксированный момент времени t на последовательность импульсов ( 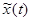) можно вычислить по формуле (принцип наложения):

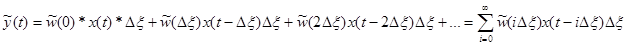. (3-24)

Точное решение можно найти при 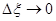, тогда 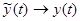, , 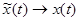, 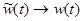а сумма переходит в интеграл. Таким образом, можно записать:

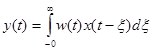. (3-25)

ИПХ должна удовлетворять условию физической реализуемости, то есть, равняться нулю при t<0, поэтому без потери смысла можно записать выражение 5-5 следующим образом:

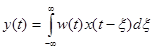. (3-26)

Если воздействие внезапно приложено в нулевой момент времени, и начальные условия нулевые, то можно записать:

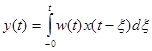. (3-27)

Выражение (5-7) называется интеграл свертки.

Если входное воздействие представляет собой функцию Хевисайда, то можно получить выражение для переходной характеристики:

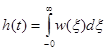. (3-28)

Необходимо заметить, что ИПХ – это производная от ПХ.

Из интеграла свертки следует, что выходная величина динамической системы в некоторый момент времени зависит не только от входного воздействия в этот момент времени, но и в предыдущие моменты времени. То есть, динамическая система обладает «памятью» на входные воздействия, статическая – не обладает.