Преобразование Лапласа

Дифференциальные уравнения можно решать различными способами; рассмотрим методы решения неоднородных линейных дифференциальных уравнений. Их можно решать методом вариации произвольных постоянных или операторным методом (то есть, с помощью преобразования Лапласа). Рассмотрим последний метод.

С помощью преобразования Лапласа каждой функции в пространстве оригиналов ставится в соответствие некая функция в пространстве изображений. Переход от оригинала к изображению выполняется по формуле:

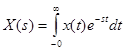, (3-6)

где: 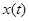- оригинал, ;

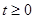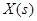- изображение функции-оригинала.

Переменная s является комплексной и имеет вид 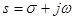. Изображение по Лапласу обозначается:

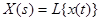. (3-7)

Рассмотрим пример. Пусть 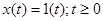- данная функция называется функцией Хевисайда, она равна нулю при 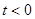и единице во всех остальных случаях, то есть, представляет собой единичную ступеньку, возникающую в момент времени .

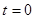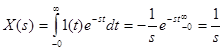. (3-8)

Прочие примеры приведены в учебнике В.Я. Ротача. Изображение основных функций по Лапласу необходимо выучить наизусть.