Дискретное преобразование Фурье

Спектральная плотность дискретизированного сигнала 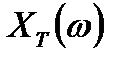является непрерывной периодической функцией частоты с периодом .

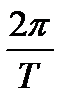Рисунок 1.1 – дискретизация сигнала по времени и по спектру

Однако для цифровой обработки требуется дискретизация сигнала не только во временной области, но и в частотной.

Для этого сплошной спектр 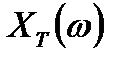должен быть представлен совокупностью своих дискретных значений .

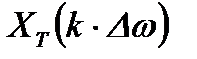Такой спектр может быть получен в результате периодического повторения последовательности 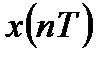с периодом .

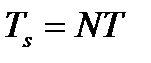В этом случае интервал между соседними спектральными составляющими равен:

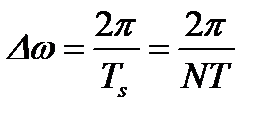. (1.1)

После подстановки 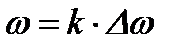получаем следующее выражение для спектральной плотности (с учетом перехода от бесконечной последовательности к конечной длительностью ):

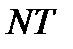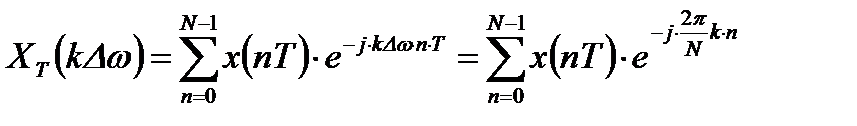, (1.2)

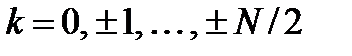(для четного N).

Выражение (1.2) называют дискретным преобразованием Фурье (ДПФ), которое обычно записывается через аргументы 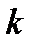и :

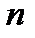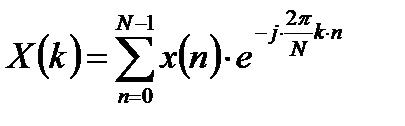, (1.3)

.

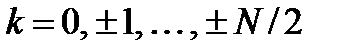С учетом периодичности ДПФ его можно записывать следующим образом:

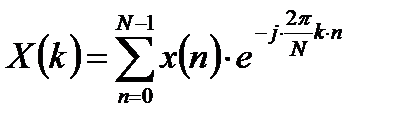, (1.4)

.

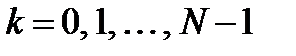Можно показать, что обратное дискретное преобразование Фурье (ОДПФ) записывается в виде:

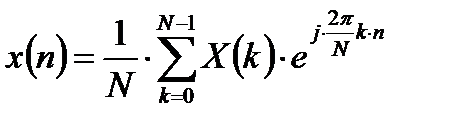, (1.5)

.

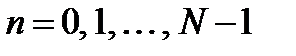Таким образом, дискретизированному сигналу 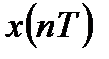соответствует сплошной спектр 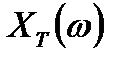с периодической структурой. Дискретизированному спектру 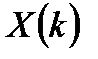соответствует периодическая последовательность сигналов 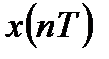, повторяемых с периодом N.

ДПФ является линейным преобразованием, трансформирующим вектор временных отсчетов в вектор такой же длины, содержащей спектральные отсчеты. Такое преобразование может быть представлено как результат умножения некоторой квадратной матрицы на входной вектор-столбец:

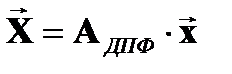, (1.6)

где 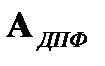- матрица преобразования.

Общая формула для элемента матрицы ДПФ, расположенного в 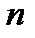- м столбце 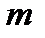-й строки имеет вид:

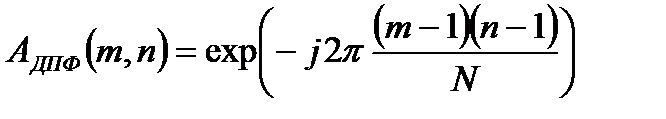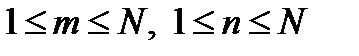, . (1.7)

Например, при 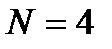матрица преобразования ДПФ запишется следующим образом:

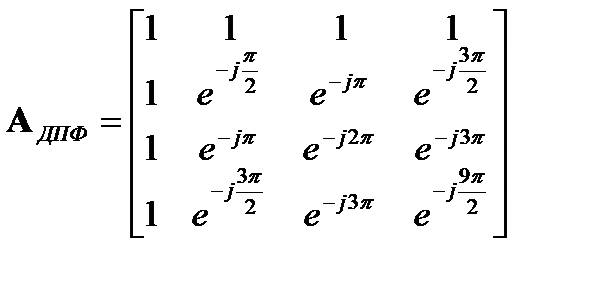. (1.8)