Модель дискретного и дискретизированного сигналов во временной области
Дискретный сигнал 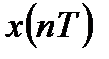 представляет собой последовательность отсчетов непрерывного сигнала
представляет собой последовательность отсчетов непрерывного сигнала 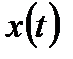 , взятая с интервалом дискретизации
, взятая с интервалом дискретизации 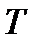 :
:
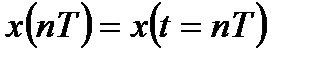 , (1.1)
, (1.1)
Представление (1) иногда называют решетчатой функцией.
Однако таким образом определенный дискретный сигнал неудобен при выполнении классического спектрального анализа, который предполагает использование операции интегрирования над функцией времени, а не над последовательностью чисел.
В этой связи вводят дискретизированный сигнал 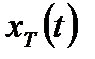 , как функцию времени и процедуру дискретизации представляют в виде произведения исходной функции
, как функцию времени и процедуру дискретизации представляют в виде произведения исходной функции 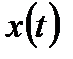 на вспомогательную периодическую последовательность
на вспомогательную периодическую последовательность 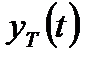 достаточно коротких тактовых импульсов. В качестве таких импульсов рассматривают прямоугольные импульсы амплитудой
достаточно коротких тактовых импульсов. В качестве таких импульсов рассматривают прямоугольные импульсы амплитудой 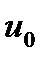 и длительности
и длительности 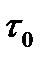 , малой по сравнению с периодом дискретизации
, малой по сравнению с периодом дискретизации 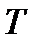 :
:
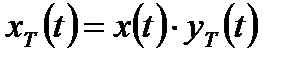 . (1.2)
. (1.2)
Если с уменьшением длительности тактовых импульсов 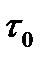 одновременно увеличивать их амплитуду
одновременно увеличивать их амплитуду 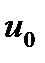 , чтобы выполнялось условие
, чтобы выполнялось условие 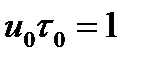 , то тактовая последовательность примет вид последовательности дельта-функций:
, то тактовая последовательность примет вид последовательности дельта-функций:
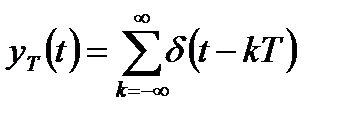 . (1.3)
. (1.3)
Тогда выражение (2) изменится следующим образом:
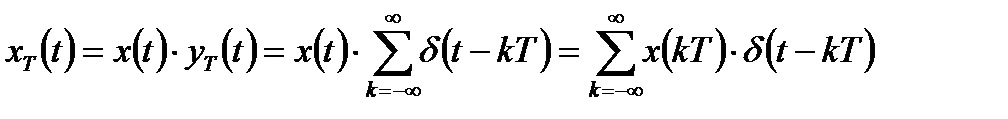 . (1.4)
. (1.4)
Таким образом, дискретизированный сигнал приобретает вид последовательности дельта-функций с весовыми коэффициентами, равными значениям сигнала 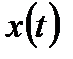 в дискретные моменты времени
в дискретные моменты времени 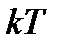 .
.
Рисунок 1.1 – дискретизация сигнала
Спектр таким образом определенного дискретизированного сигнала 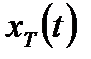 будем обозначать как
будем обозначать как 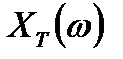 в отличие от обычно используемого классического спектра
в отличие от обычно используемого классического спектра 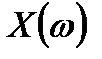 для исходного непрерывного сигнала
для исходного непрерывного сигнала 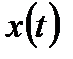 .
.
Дата добавления: 2017-09-19; просмотров: 918;
