Связь спектра дискретизированного сигнала со спектром исходного сигнала. Теорема Котельникова.
2.2.3.1. Связь спектра дискретизированного сигнала со спектром исходного сигнала
Таким образом, спектр дискретизированного сигнала 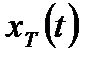 описывается выражением (2.8):
описывается выражением (2.8):
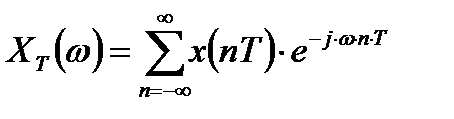 .
.
Найдем связь между спектром дискретизированного сигнала 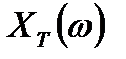 и спектром исходного сигнала
и спектром исходного сигнала 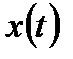 до его дискретизации
до его дискретизации 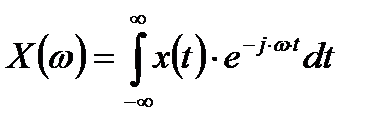 .
.
Для этого учтем выражение для обратного преобразования Фурье 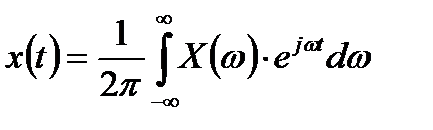 . Соответственно, для дискретных значений сигнала можно записать следующую связь со спектром исходного непрерывного сигнала
. Соответственно, для дискретных значений сигнала можно записать следующую связь со спектром исходного непрерывного сигнала 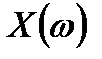 :
:
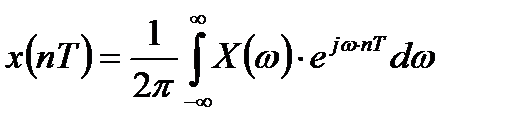 .
.
Подставим это соотношение в выражение для спектра дискретизированного сигнала:
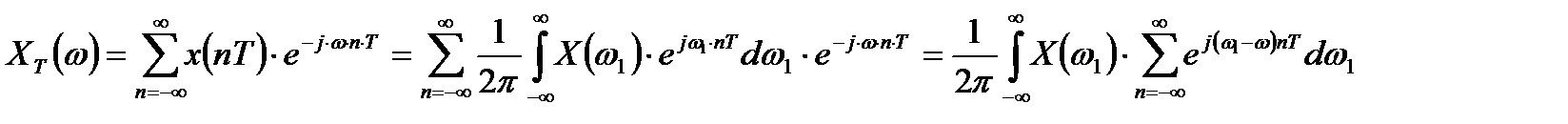 .
.
Учтем, что
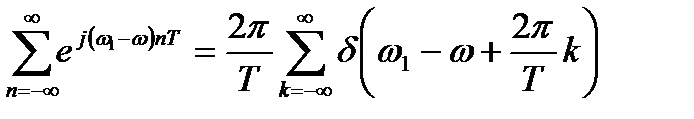 .
.
Воспользуемся фильтрующим свойством дельта-функции, в соответствии с которым:
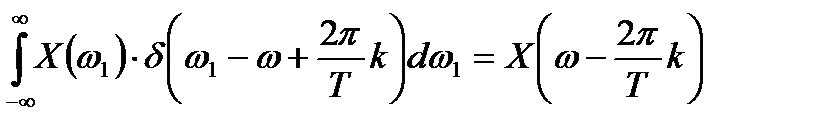 .
.
Таким образом, можно записать следующее выражение, которое характеризует связь спектра дискретизированного сигнала со спектром исходного непрерывного сигнала:
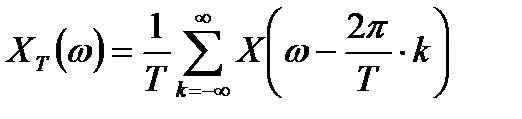 . (3.1)
. (3.1)
Таким образом, спектр дискретизированного сигнала представляет собой периодическую последовательность на оси частот с периодом 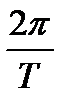 спектров исходного непрерывного сигнала.
спектров исходного непрерывного сигнала.
2.2.3.2. Восстановление исходного непрерывного сигнала. Теорема Котельникова.
Если исходный непрерывный сигнал 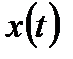 ограничен верхней граничной частотой
ограничен верхней граничной частотой
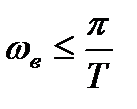 ,
,
то отдельные копии спектра 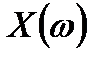 не накладываются друг на друга в спектре дискретизированного сигнала.
не накладываются друг на друга в спектре дискретизированного сигнала.
Рисунок 3.1 – восстановление исходного непрерывного сигнала
В этом случае аналоговый сигнал 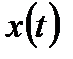 , подвергшийся дискретизации, в соответствии с теоремой Котельникова может быть полностью восстановлен с помощью идеального ФНЧ, имеющего прямоугольную АЧХ:
, подвергшийся дискретизации, в соответствии с теоремой Котельникова может быть полностью восстановлен с помощью идеального ФНЧ, имеющего прямоугольную АЧХ:
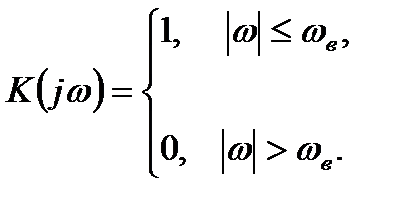
Импульсная характеристика такого фильтра является обратным преобразованием Фурье от частотной характеристики:
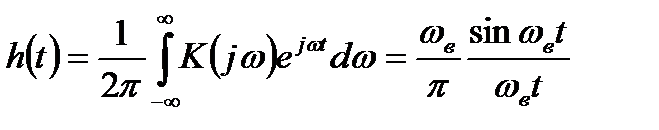 .
.
В этом случае в соответствии с интегралом Дюамеля можно восстановить исходный ограниченный по спектру сигнал в базисе Котельникова с точностью до постоянного множителя:
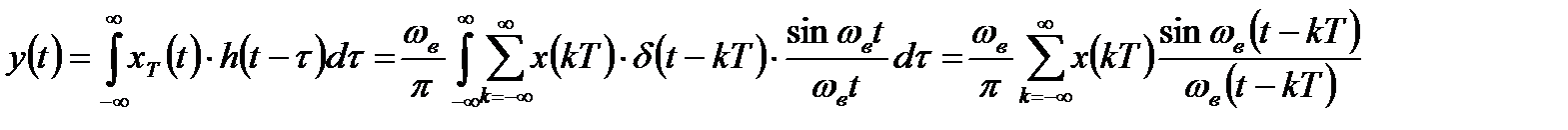 . (3.2)
. (3.2)
Точная формулировка теоремы Котельникова имеет следующий вид: произвольный сигнал, спектр которого не содержит частот выше 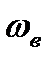 , может быть полностью восстановлен, если известны дискретные значения этого сигнала, взятые через равные промежутки времени
, может быть полностью восстановлен, если известны дискретные значения этого сигнала, взятые через равные промежутки времени 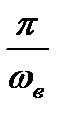 .
.
2.2.4. Z – преобразование дискретных сигналов
2.2.4.1. Определение z – преобразования
При математическом описании дискретных сигналов в выражении для спектра 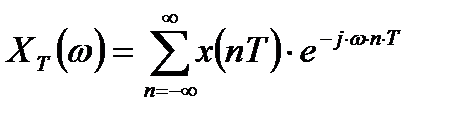 важную роль играет функция
важную роль играет функция 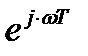 , которая при преобразованиях возводится в целую степень
, которая при преобразованиях возводится в целую степень 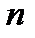 . Однако эта функция является трансцендентной функцией частоты
. Однако эта функция является трансцендентной функцией частоты 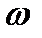 , что существенно усложняет спектральный анализ. Для упрощения анализа вводят новую переменную
, что существенно усложняет спектральный анализ. Для упрощения анализа вводят новую переменную 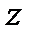 , которая связана с частотой
, которая связана с частотой 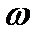 выражением:
выражением:
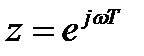 .
.
При такой замене спектр дискретизированного сигнала преобразуется в рациональную функцию переменной 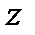 :
:
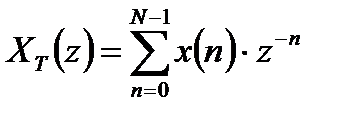 , (4.1)
, (4.1)
где 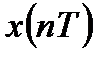 - оригинал
- оригинал 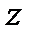 - преобразования;
- преобразования;
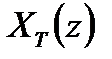 -
- 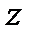 - изображение функции
- изображение функции 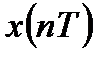 .
.
Полученное выражение называется прямым двухсторонним 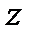 - преобразованием (одностороннее преобразование суммируется от 0 и совпадает с двухсторонним только для последовательностей, равных нулю для отрицательных значений аргумента
- преобразованием (одностороннее преобразование суммируется от 0 и совпадает с двухсторонним только для последовательностей, равных нулю для отрицательных значений аргумента 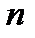 ).
).
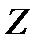 - преобразование дискретных сигналов является аналогом преобразования Лапласа для непрерывных сигналов. Вводится для:
- преобразование дискретных сигналов является аналогом преобразования Лапласа для непрерывных сигналов. Вводится для:
- полезно иметь дискретный аналог преобразования Лапласа, справедливый для более широкого класса сигналов;
- при аналитических исследованиях и расчетах пользоваться 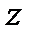 - преобразованием более удобно.
- преобразованием более удобно.
Пример z – преобразования
Пусть необходимо получить z – изображение дискретного единичного скачка:
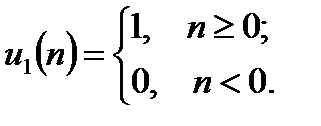
В результате применения z – преобразования к дискретному единичному скачку можно получить:
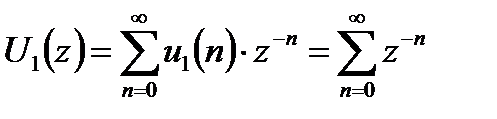 .
.
Таким образом, полученное выражение представляет собой сумму бесконечной геометрической прогрессии:
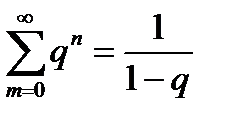
при 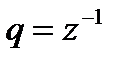 .
.
Соответственно, z – изображение дискретного единичного скачка имеет вид:
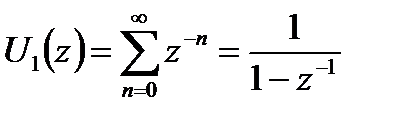 .
.
2.2.4.2. Свойства z – преобразования
1. Линейность:
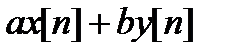 имеет z-преобразование
имеет z-преобразование 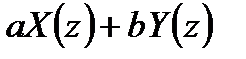 .
.
2. Задержка:
Последовательность 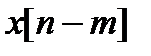 имеет Z-преобразование
имеет Z-преобразование 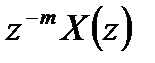 .
.
3. Обращение во времени:
Последовательность 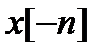 имеет z-преобразование
имеет z-преобразование 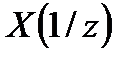 .
.
4. Масштабирование:
Последовательность 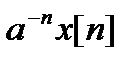 имеет z-преобразование
имеет z-преобразование 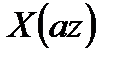 .
.
5. Свертка:
Последовательность 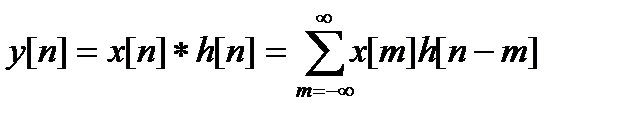 , характеризующая связь выходного сигнала через входной через импульсную характеристику дискретного фильтра
, характеризующая связь выходного сигнала через входной через импульсную характеристику дискретного фильтра 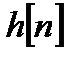 , имеет Z-преобразование:
, имеет Z-преобразование:
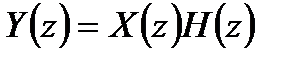 .
.
2.2.4.3. Обратное z – преобразование
Отыскание оригинала по заданному изображению 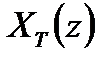 производится с помощью обратного z – преобразования:
производится с помощью обратного z – преобразования:
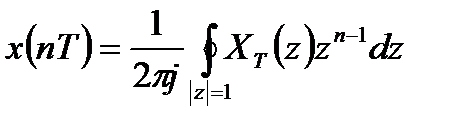 . (4.2)
. (4.2)
Непосредственное вычисление интеграла (4.2) сложно или невозможно. Поэтому на практике обратное z-преобразование получают более простыми способами:
1. С использованием таблицы соответствий;
2. На основании теоремы Коши о вычетах;
3. Разложение изображения 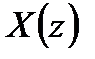 на простые дроби.
на простые дроби.
Обратное z-преобразование удобно использовать при отыскании отклика дискретной системы на дискретный сигнал и при отыскании импульсной характеристики дискретной системы при известной ее передаточной функции.
Для вычисления обратного z-преобразования с использованием таблицы соответствий в справочнике, содержащем таблицы оригиналов и соответствующих им изображений, находят оригинал для заданного изображения: Таблица 4.1. Достоинством способа является отсутствие необходимости вычисления обратного z-преобразования: просто анализируются результаты прямого z-преобразования для выбранных оригиналов. При вычислении прямого z-преобразования как правило используют выражение для суммы членов геометрической прогрессии и свойства z-преобразования. Недостатком способа является ограниченное число изображений в таблице.
Если z-изображение отсутствует в таблице соответствий, можно использовать разложение изображения на простые дроби. Например:
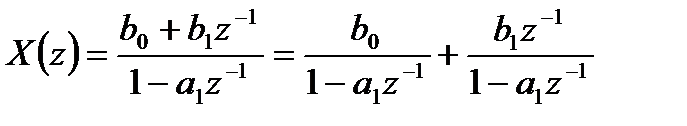 .
.
В этом случае, пользуясь свойством линейности z – преобразования и Таблицей 4.1 можно получить:
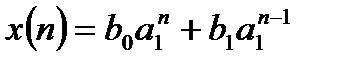 .
.
Таблица 4.1. Таблица соответствия
Последовательность 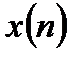
| z-изображение | |
| 1. | 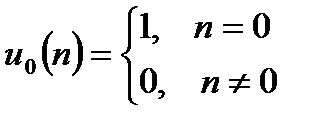
| |
| 2. | 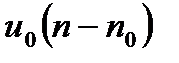
| 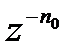
|
| 3. | 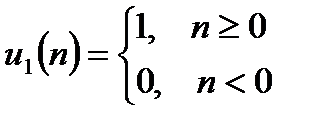
| 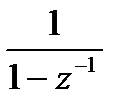
|
| 4. | 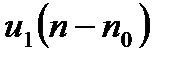
| 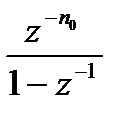
|
| 5. | 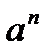
| 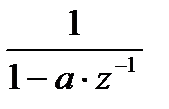
|
| 6. |
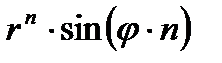
| 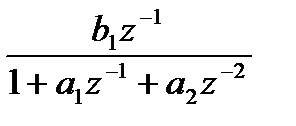 ; ;
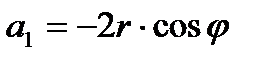 ; ;
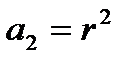 ; ;
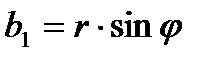 . .
|
| 7. |
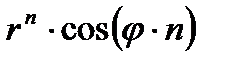
| 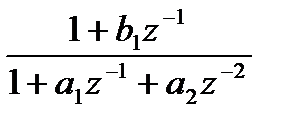 ; ;
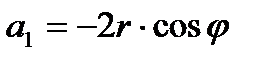 ; ;
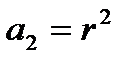 ; ;
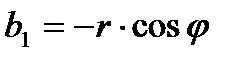 . .
|
Вычисление обратного z – преобразования с использованием вычетов основано на теореме Коши. Суть теоремы заключается в том, что интеграл вида (4.2), позволяющий вычислить обратное z – преобразование, вычисляется как сумма вычетов во всех особых точках (полюсах):
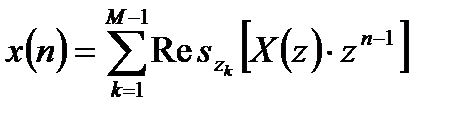 , (4.3)
, (4.3)
где 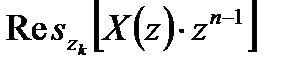 - вычет функции
- вычет функции 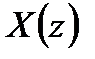 в k-ом полюсе
в k-ом полюсе 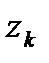 .
.
Например, для изображения 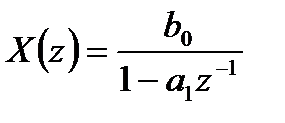 имеется один полюс
имеется один полюс 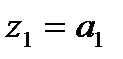 . Поэтому для получения обратного z – преобразования необходимо вычислить только один вычет:
. Поэтому для получения обратного z – преобразования необходимо вычислить только один вычет:
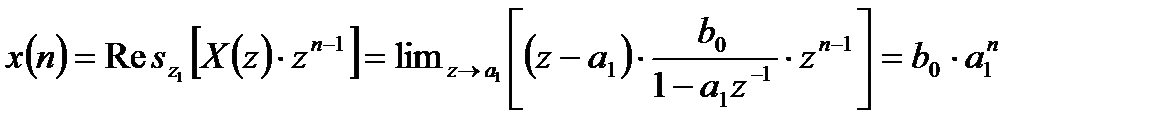 .
.
Дата добавления: 2017-09-19; просмотров: 1785;
