Связь КЧХ и временных динамических характеристик

Зная КЧХ динамической системы можно вычислить ее импульсную переходную характеристику:

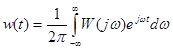. (7-9)

Воспользовавшись формулой Эйлера и выразив КЧХ через действительную и мнимую части, получим:

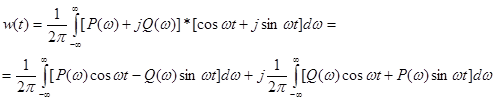. (7-10)

Так как в левой части (7-10) находится вещественная функция, в правой части тоже должна находиться вещественная функция, таким образом, второе слагаемое правой части равняется нулю. Кроме того, при t<0 импульсная переходная характеристика равна нулю по условию физической реализуемости системы. Таким образом, можно записать, что:

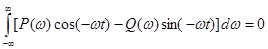. (7-11)

Из (7-11) в итоге получим:

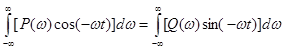. (7-12)

Из (7-12) можно выразить мнимую часть через вещественную и подставить полученное в (7-10), тогда в итоге получим:

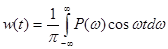. (7-13)

Так как импульсная переходная характеристика является производной от переходной характеристики, можно записать, что

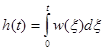. (7-14)

Воспользовавшись формулами (7-13) и (7-14) можно записать, что

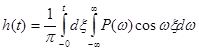. (7-14)

Выполнив необходимые преобразования (7-14), получим:

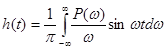. (7-15)

Учитывая, что вещественная часть КЧХ – это четная функция частоты, а также то, что для большинства рассматриваемых нами систем вещественная часть при некоторой частоте, называемой частота среза, уходит в нуль, можно записать:

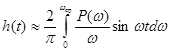. (7-16)

Необходимо также заметить, что получить переходную характеристику по формуле (7-16) можно только для систем, обладающих самовыравниванием.