Теорема 3.3. (теорема Коши).
Пусть функции 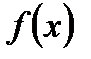 и
и 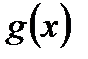 удовлетворяют следующим условиям:
удовлетворяют следующим условиям:
1. 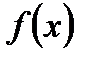 и
и 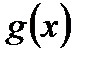 определены на сегменте
определены на сегменте 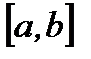 ;
;
2. 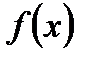 и
и 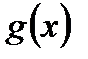 дифференцируемы на интервале
дифференцируемы на интервале 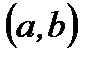 и
и 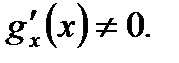
Тогда существует точка 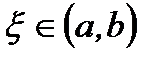 , что на интервале
, что на интервале 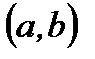 имеет место соотношение
имеет место соотношение
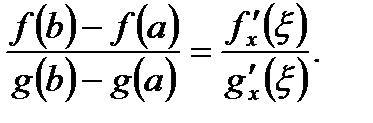 (3.45)
(3.45)
где 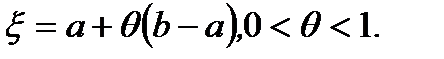
Доказательство.Составим функцию 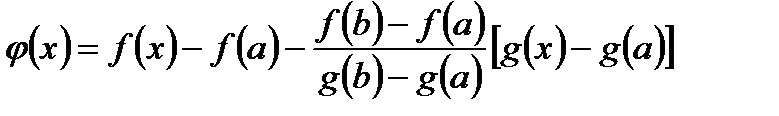 , и заметим, что она удовлетворяет всем условиям теоремы Ролля. На самом деле имеем:
, и заметим, что она удовлетворяет всем условиям теоремы Ролля. На самом деле имеем:
1.  определена на
определена на  ;
;
2. 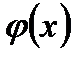 дифференцируема на
дифференцируема на 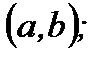
3. 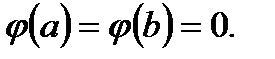
Тогда по теореме Ролля существует точка 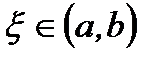 , что
, что
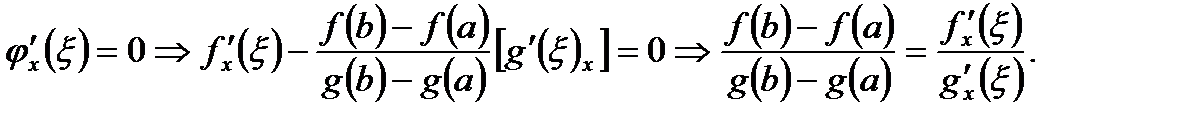 (3.46)
(3.46)
Отметим, что если 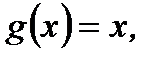 то из (3.46) получим формулу Лагранжа (3.43).
то из (3.46) получим формулу Лагранжа (3.43).
При исследовании поведения сложной функции вокруг точки 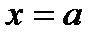 имеет смысл, если это возможно, представить эту функцию в виде суммы степенных функций с определенными коэффициентами. Особенно это актуально, когда в рассматриваемой задаче существует малый параметр. Известные математики Тейлор и Маклорен показали, что такая возможность есть.
имеет смысл, если это возможно, представить эту функцию в виде суммы степенных функций с определенными коэффициентами. Особенно это актуально, когда в рассматриваемой задаче существует малый параметр. Известные математики Тейлор и Маклорен показали, что такая возможность есть.
Если функция 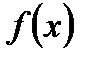 дифференцируема
дифференцируема 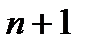 раз в некоторой окрестности точки
раз в некоторой окрестности точки 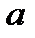 , то она может быть представлена в виде суммы многочлена степени
, то она может быть представлена в виде суммы многочлена степени 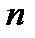 по формуле Тейлора и остаточного члена
по формуле Тейлора и остаточного члена 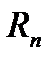 , например, в форме Лагранжа:
, например, в форме Лагранжа:
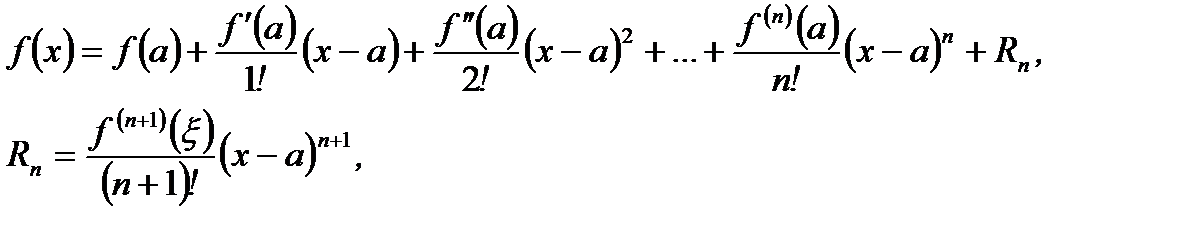 (3.47)
(3.47)
где 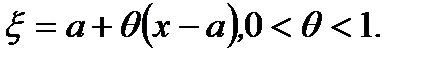 При
При 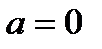 из формулы (3.47) получим формулу Маклорена
из формулы (3.47) получим формулу Маклорена
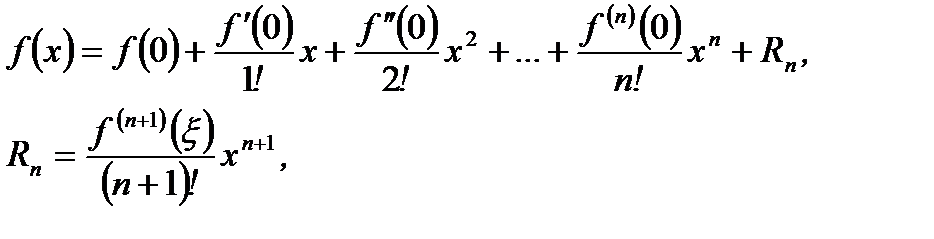 (3.48)
(3.48)
где 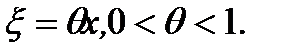
Пример 3.49. Разложить по формуле Маклорена (3.48) функцию 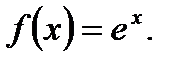
Решение.Имеем
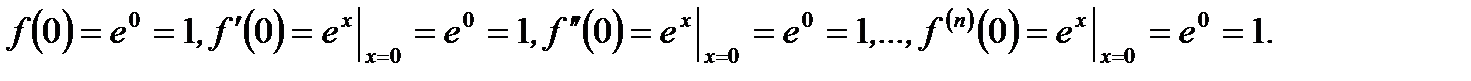 (3.49)
(3.49)
Подставляя (3.49) в (3.48), получим
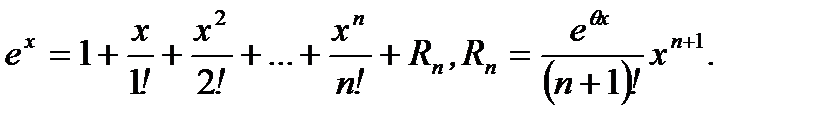 (3.50)
(3.50)
Ответ: 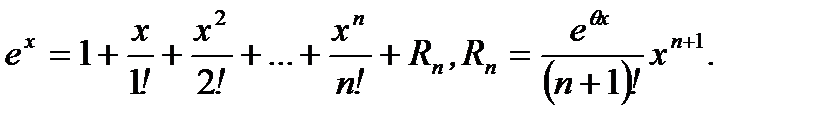
Аналогично можно получить разложения по формуле Маклорена для следующих функций:
1. 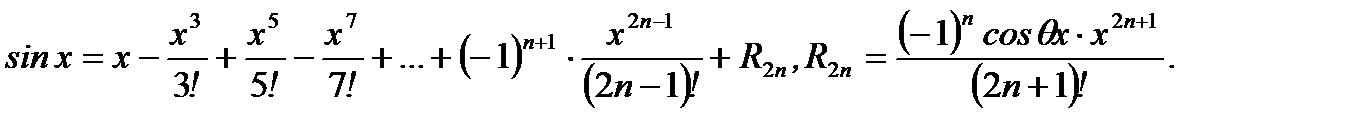 (3.51)
(3.51)
2. 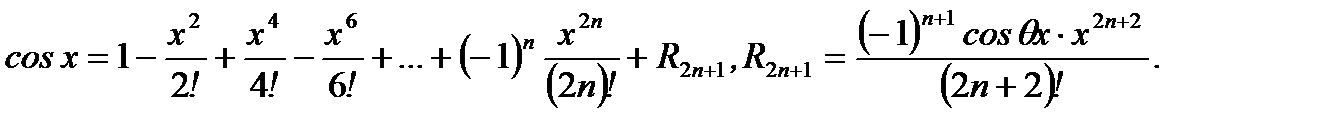 (3.52)
(3.52)
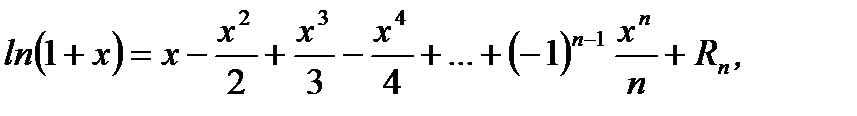
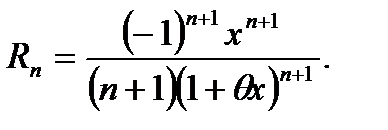 (3.53)
(3.53)
3. 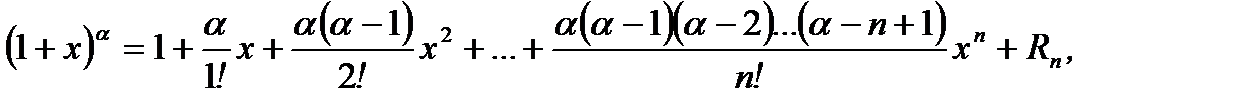 (3.54)
(3.54)
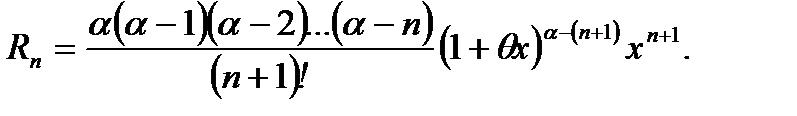
Пример 3.50. Разложить по формуле Тейлора (3.47) функцию 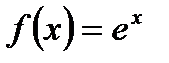 вокруг точки
вокруг точки 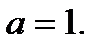
Решение.Имеем
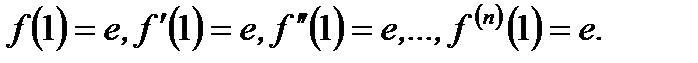 (3.55)
(3.55)
Подставляя (3.55) в (3.47), получим
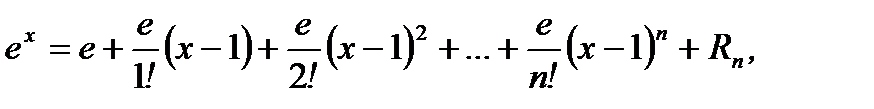 (3.56)
(3.56)
где остаточный член 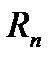 в форме Пеано выражается формулой
в форме Пеано выражается формулой 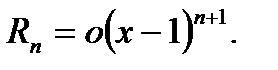 Последнее означает, что остаточный член более высокого порядка малости по сравнению с бесконечно малой
Последнее означает, что остаточный член более высокого порядка малости по сравнению с бесконечно малой 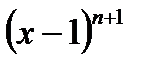 при
при 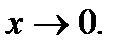
Ответ: 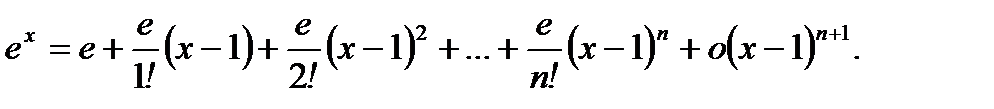
Пример 3.51.Дана кривая 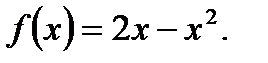 На дуге
На дуге 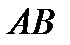 этой кривой найти точку
этой кривой найти точку 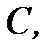 в которой касательная параллельна хорде
в которой касательная параллельна хорде 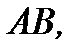 если
если 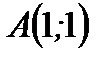 и
и 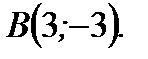
Решение.Функция 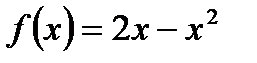 дифференцируема при всех значениях
дифференцируема при всех значениях 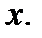 По теореме Лагранжа между
По теореме Лагранжа между 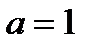 и
и 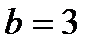 существует точка
существует точка 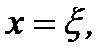 в которой имеет место равенство
в которой имеет место равенство
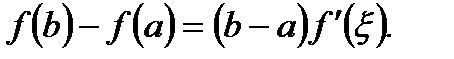 (3.57)
(3.57)
Подставляя в (3.57) соответствующие данные, получим
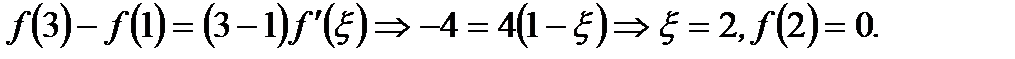
Итак, точка  имеет координаты
имеет координаты 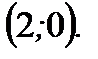
Ответ: 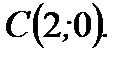
Задачи с ответами.
3.4.1. Вычислить предел
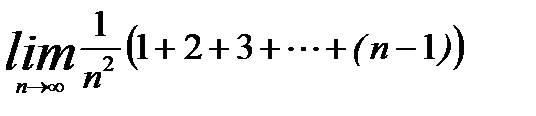 .
.
Ответ: 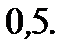
3.4.2. Вычислить предел
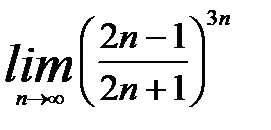 .
.
Ответ: 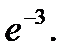
3.4.3. Вычислить предел
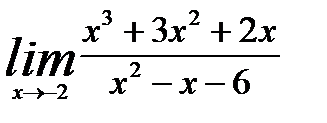 .
.
Ответ: 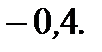
3.4.4. Вычислить предел
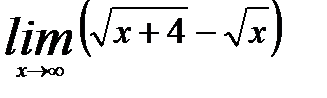 .
.
Ответ: 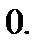
3.4.5. Вычислить предел
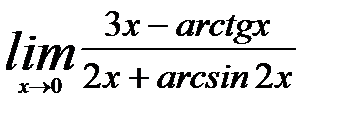 .
.
Ответ: 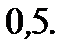
3.4.6. Вычислить предел
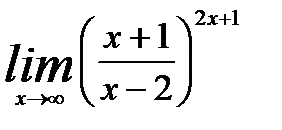 .
.
Ответ: 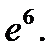
3.4.7. Исследовать функцию на непрерывность
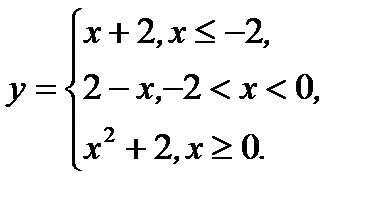
Ответ:Разрыв первого родапри 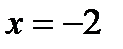 .
.
3.4.8. Найти производную по 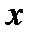 второго порядка
второго порядка
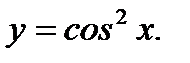
Ответ: 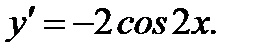
3.4.9. Найти производную по 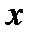 пятого порядка, применяя формулу Лейбница
пятого порядка, применяя формулу Лейбница
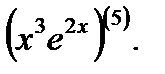
Ответ: 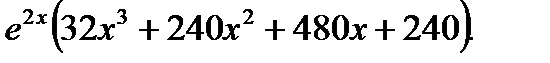
3.4.10. Вычислить предел, пользуясь правилами Лопиталя
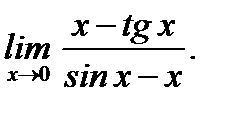
Ответ: 
3.4.11. Разложить функцию 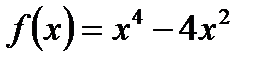 по степеням
по степеням 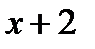 , пользуясь формулой Тейлора.
, пользуясь формулой Тейлора.
Ответ: 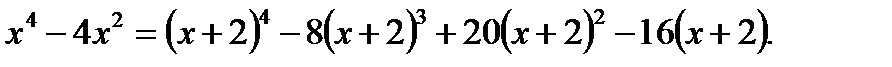
3.4.12. Найти экстремумы (max и min) данной функции
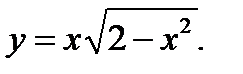


Ответ: 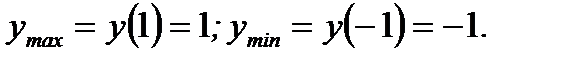
3.4.13. Найти асимптоты данной линии
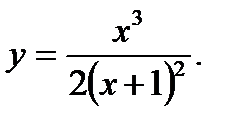
Ответ: 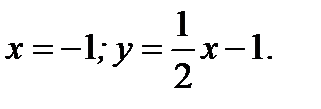
3.4.14. Функция полных издержек  в зависимости от объема выпускаемой продукции
в зависимости от объема выпускаемой продукции  задана соотношением:
задана соотношением: 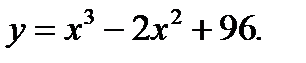 При каком объеме производства предельные и средние издержки совпадают?
При каком объеме производства предельные и средние издержки совпадают?
Ответ: 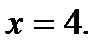
3.4.15. Завод производит 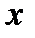 единиц продукции в месяц, при этом издержки производства определяются формулой
единиц продукции в месяц, при этом издержки производства определяются формулой 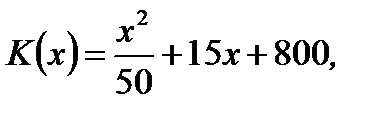 а цена –
а цена – 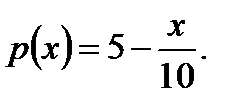 При каком объеме продукции прибыль будет максимальной? Какова при этом цена продукции?
При каком объеме продукции прибыль будет максимальной? Какова при этом цена продукции?
Ответ: 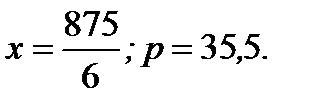
Дата добавления: 2018-11-25; просмотров: 573;
