Непрерывность функции в точке. Классификация разрывов.

Определение 3.5.Функция 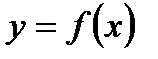называетсянепрерывной в точке 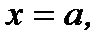если удовлетворяется условие

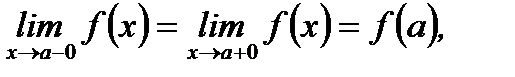(3.16)

где левосторонний и правосторонний пределы конечные числа. Если в (3.16) что-то нарушается, то функция терпит разрыв. Ниже приведена классификация разрывов.

1. Устранимый разрыв.

Функция не определена в точке 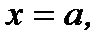но существуют конечные односторонние пределы в данной точке и они равны, то есть 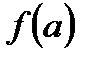–нет, но 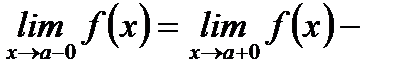конечные числа.

Пример 3.24.Функция 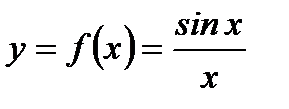имеет устранимый разрыв в точке 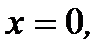так как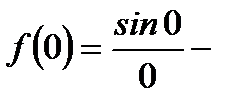нет, а 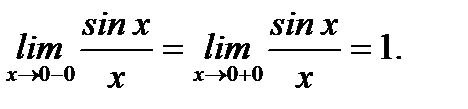Если на основании этой функции определить новую функцию 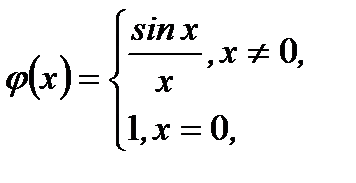тоона будетнепрерывнойвточке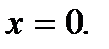

2. Разрыв первого рода.

Если конечные левосторонний и правосторонний пределы функции в точке 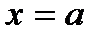не равны,тофункция в точке 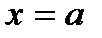имеет разрыв первого рода.

Пример 3.25.Знаковая функция

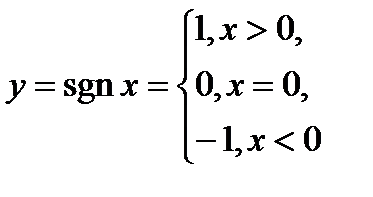
в точке 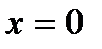имеет разрыв первого рода, так как 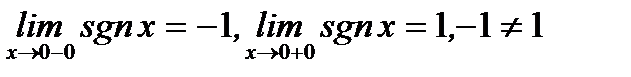(см. рис. 3.3).

3. Разрыв второго рода.

Если хотя бы один из односторонних пределов функции в точке 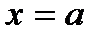бесконечный, или в точке 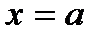вообще нет никакого предела, то функция имеет в точке 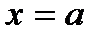разрыв второго рода.

Пример 3.26.Функция 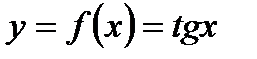,например, в точке 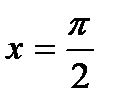имеет разрыв второго рода или бесконечный разрыв, так как 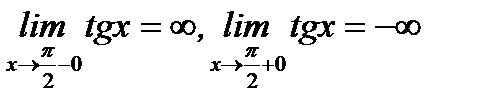.А, например, функция 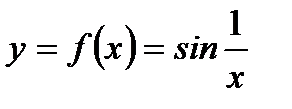в точке 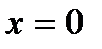вообще никакого предела не имеет. Она в точке 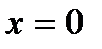терпитразрыв второго рода.

Пример 3.27.Исследовать на непрерывность функцию (рисунок 3.6)

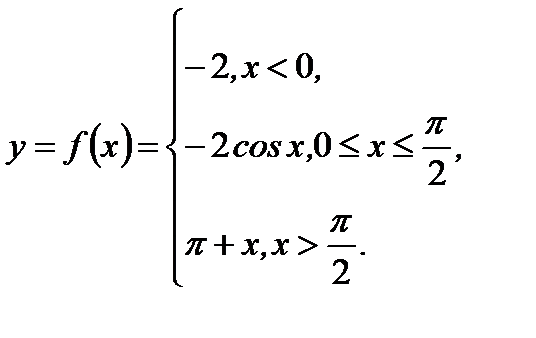
Решение.Проверим условие непрерывности в точках 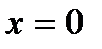и

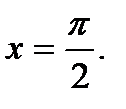
1.

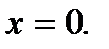
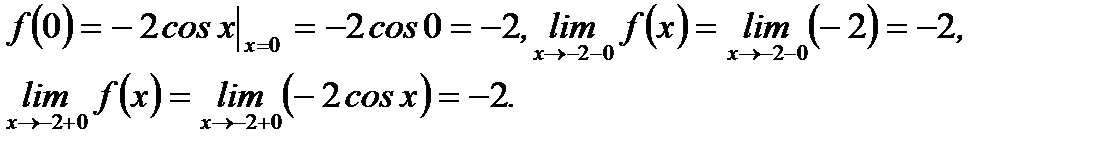(3.17)

Как видно из (3.17), в точке 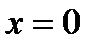выполняется условие непрерывности, то есть в этой точке функция непрерывна.

2.

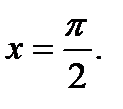
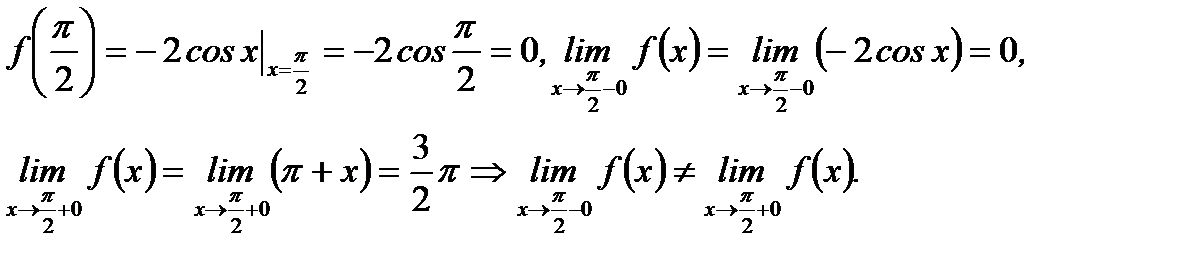(3.18)

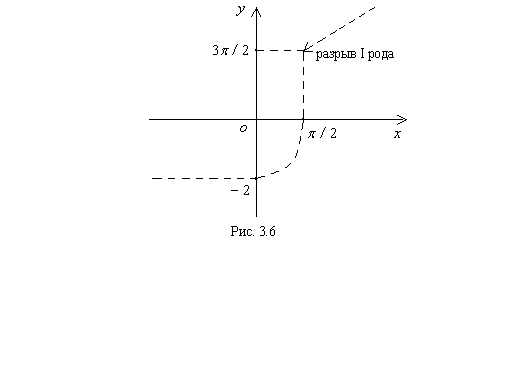
(3.18) указывает на то, что в точке 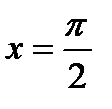функция терпит разрыв I рода.