Дифференциальное исчисление функции одной переменной.
3.3.1. Производная и дифференциал. Правила Лопиталя.
При исследовании неравномерных процессов различной природы (неравномерное движение тела, неравномерный процесс производства и т.д.) возникает вопрос: как найти интересующие нас величины в неравномерных процессах? Например, если тело движется равномерно с постоянной скоростью, то в любой момент времени скорость (мгновенная скорость) определяется формулой 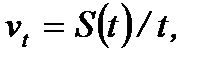 где
где 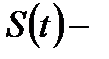 пройденный путь,
пройденный путь, 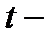 время. А если тело движется не с постоянной скоростью, то мгновенную скорость в любой момент времени
время. А если тело движется не с постоянной скоростью, то мгновенную скорость в любой момент времени 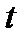 нельзя найти по указанной выше формуле. В таком случае рассматриваем элементарный (маленький) промежуток времени
нельзя найти по указанной выше формуле. В таком случае рассматриваем элементарный (маленький) промежуток времени 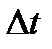 , в течение которого тело пройдет элементарный (маленький) путь
, в течение которого тело пройдет элементарный (маленький) путь 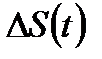 (рисунок 3.7).
(рисунок 3.7).

Так как 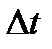 и
и 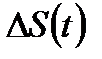 малые величины, то можно считать, что тело движется с постоянной
малые величины, то можно считать, что тело движется с постоянной
скоростью. Тогда 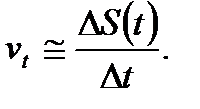 Очевидно, что для получения точного значения мгновенной скорости в момент времени
Очевидно, что для получения точного значения мгновенной скорости в момент времени 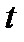 , мы должны
, мы должны 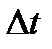 стремить к нулю, то есть
стремить к нулю, то есть
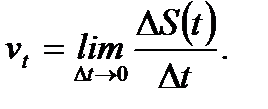 (3.19)
(3.19)
Далее конечный предел (3.19) математики называют производной первого порядка от 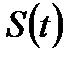 и обозначают как
и обозначают как 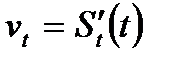 , или
, или 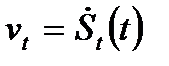 , или
, или  Аналогично, для нахождения издержек на изготовление
Аналогично, для нахождения издержек на изготовление 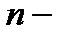 ого продукта при неравномерном процессе производства нужно пользоваться понятием производной.
ого продукта при неравномерном процессе производства нужно пользоваться понятием производной.
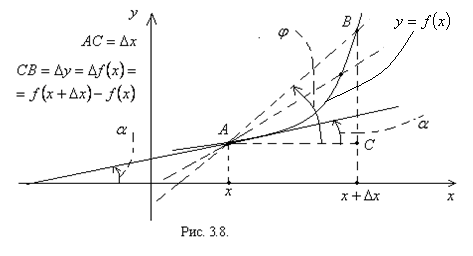
Теперь перейдем к более корректному математическому определению производной функции 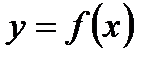 в точке. Пусть дана функция
в точке. Пусть дана функция 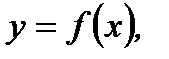 которая определена и непрерывна в некоторой окрестности точки
которая определена и непрерывна в некоторой окрестности точки 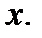 Дадим аргументу
Дадим аргументу  положительное приращение
положительное приращение 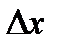
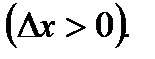 Тогда функция
Тогда функция 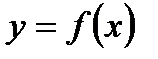 также получит приращение
также получит приращение 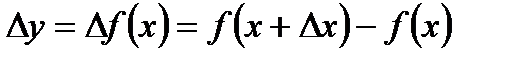 (рис. 3.8).
(рис. 3.8).
Определение 3.6.Еслисуществует конечный предел отношения приращения функции  к приращению аргумента при стремлении к нулю приращения аргумента, то он называется производной первого порядка функции по аргументу
к приращению аргумента при стремлении к нулю приращения аргумента, то он называется производной первого порядка функции по аргументу  , и обозначается так:
, и обозначается так:
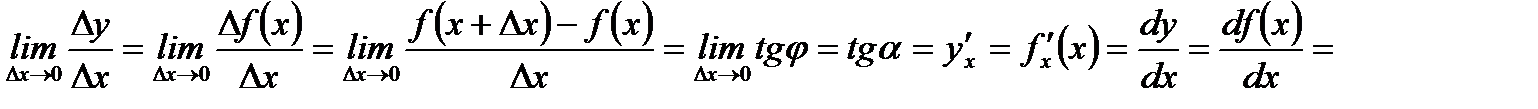

Рассмотрим две функции 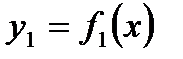 и
и 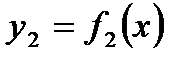 , которые имеют конечные производные в точке
, которые имеют конечные производные в точке 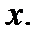 Тогда можно доказать, что их сумма, разность, произведение и частное (при условии
Тогда можно доказать, что их сумма, разность, произведение и частное (при условии 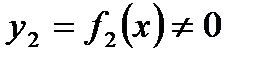 ) также имеют конечные производные, и справедливы следующие соотношения
) также имеют конечные производные, и справедливы следующие соотношения

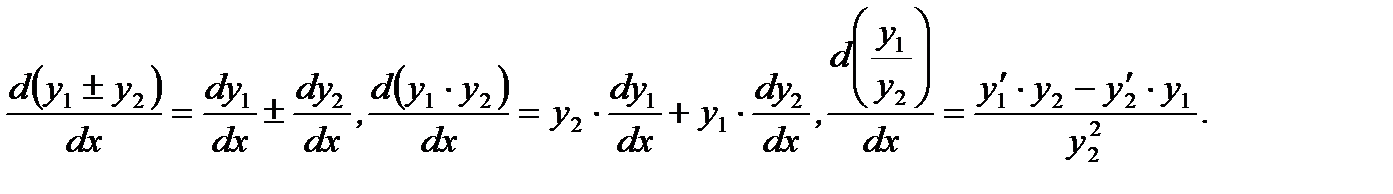 (3.20)
(3.20)
Ниже приведем доказательство, например, для случая суммы. Итак, докажем, что 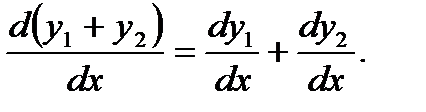

Пусть 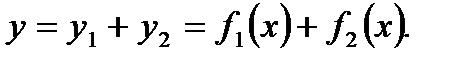 Тогда
Тогда  и
и 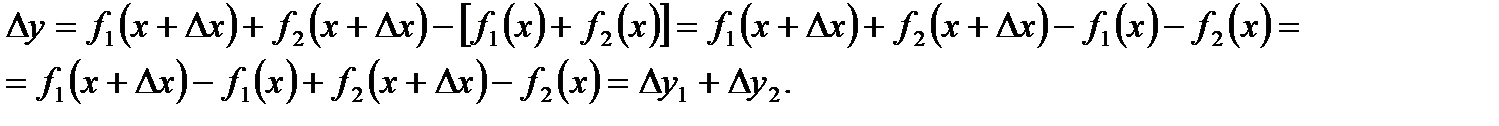
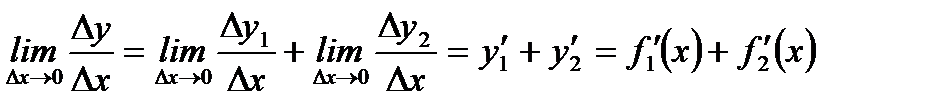 . Так как по предположению существуют
. Так как по предположению существуют  то существует и
то существует и 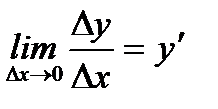 , при этом
, при этом 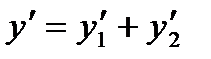 . Заметим, что аналогично можно доказать и остальные соотношения (3.20).
. Заметим, что аналогично можно доказать и остальные соотношения (3.20).
Отметим, что правила вычисления производных от элементарных функций получаются на основе определения производной (см. определение 3.6.). Ниже это показано для функций 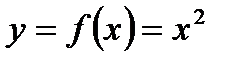 и
и 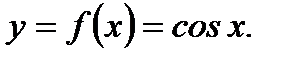
1. 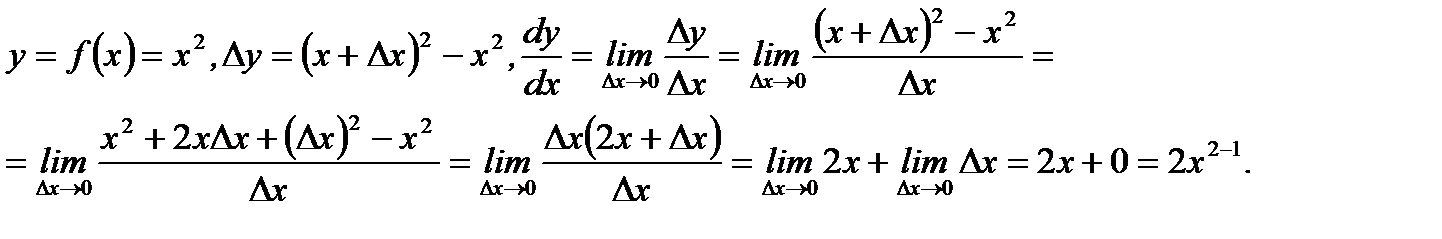
Таким образом, получили, что 
2. 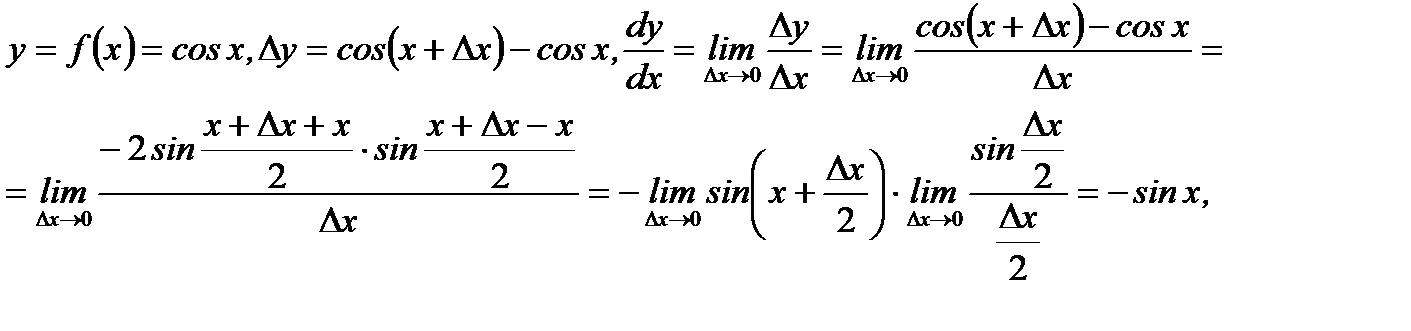
так как 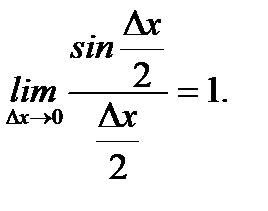 Итак получили, что
Итак получили, что 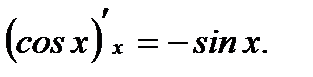
Аналогично получаются и следующие правила вычисления производных от остальных элементарных функций.
1. 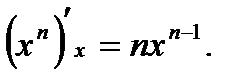 2.
2. 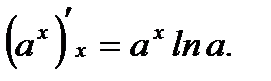 3.
3. 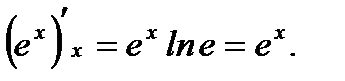 4.
4. 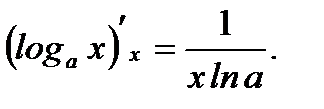
5. 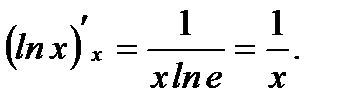 6.
6. 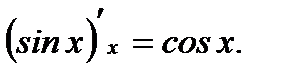 7.
7. 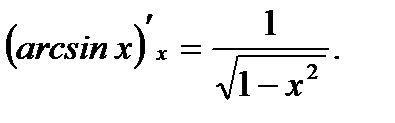 8.
8. 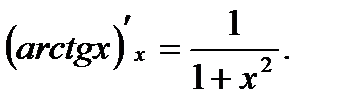
9. 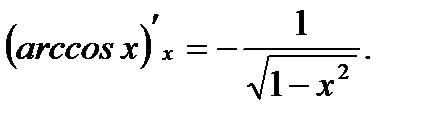 10.
10.  11.
11. 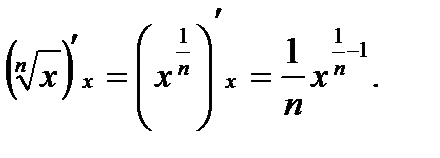
12. Если 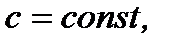 то
то 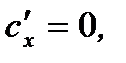 так как в этом случае
так как в этом случае 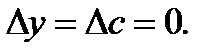 Отсюда следует любопытное свойство: постоянный множитель можно вынести из-под знака производной. На самом деле имеем
Отсюда следует любопытное свойство: постоянный множитель можно вынести из-под знака производной. На самом деле имеем 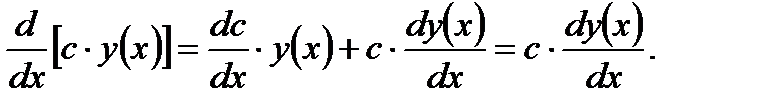
Заметим, что правила вычисления производных от элементарных функций инвариантны (не меняются) относительно аргумента. Это означает, например, что
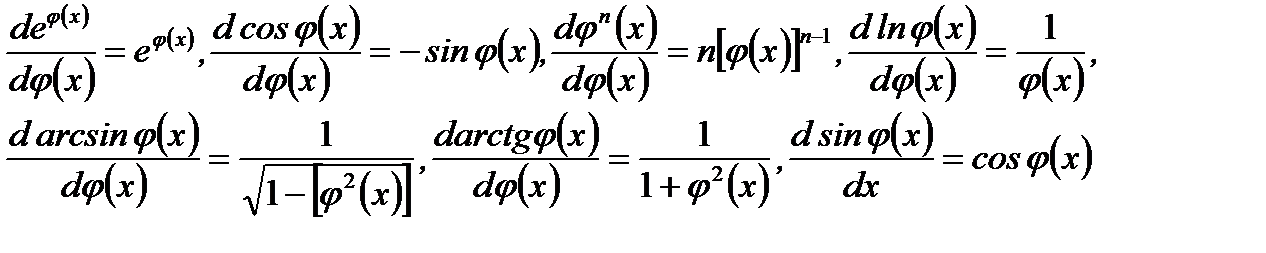
и так далее.
Определение 3.7.Если приращение функции  можно представить в виде
можно представить в виде 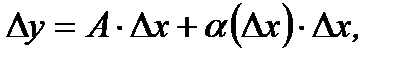 где
где 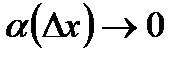 при
при 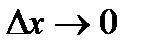 и
и 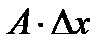 есть главная линейная часть приращения
есть главная линейная часть приращения  , то функция
, то функция 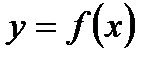 называется дифференцируемой.
называется дифференцируемой.
Пусть функция 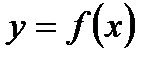 дифференцируема. Тогда
дифференцируема. Тогда 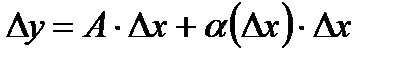 или
или 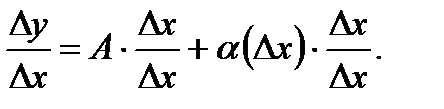 Переходя к пределу в этом выражении, когда
Переходя к пределу в этом выражении, когда 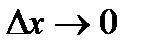 , получим
, получим
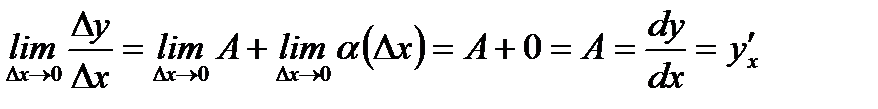 и тогда
и тогда 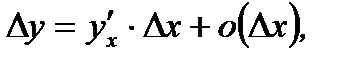 где
где 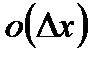 более высокого порядка бесконечно малая чем
более высокого порядка бесконечно малая чем 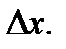
Определение 3.8.Главная линейная часть 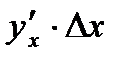 приращения функции
приращения функции 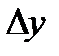 называется дифференциалом функции и обозначается как
называется дифференциалом функции и обозначается как 
Нетрудно заметить, что если 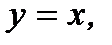 то
то 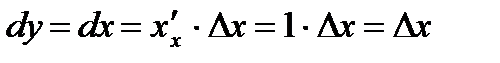 и
и 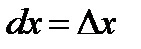 . Тогда для дифференциала функции получаем выражение
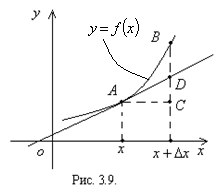
. Тогда для дифференциала функции получаем выражение  Геометрически это означает, что дифференциал функции есть приращение ординаты касательной (см. рис. 3.9, отрезок DC). Как следует из определения дифференцируемости,
Геометрически это означает, что дифференциал функции есть приращение ординаты касательной (см. рис. 3.9, отрезок DC). Как следует из определения дифференцируемости, 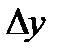 и
и  отличаются бесконечно малой величиной (
отличаются бесконечно малой величиной ( 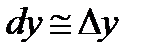 ).
).
Если задана функция  , а в свою очередь
, а в свою очередь 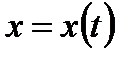 , то функция
, то функция  зависит от
зависит от 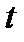 через функцию
через функцию 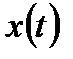 . То есть имеем дело со сложной функцией
. То есть имеем дело со сложной функцией 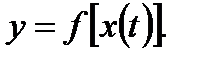 Пусть
Пусть 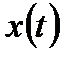 дифференцируема в точке
дифференцируема в точке 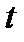 , а
, а 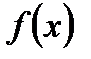 дифференцируема в точке
дифференцируема в точке 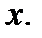 Тогда
Тогда 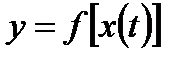 дифференцируема в точке
дифференцируема в точке 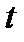 и имеет место соотношение
и имеет место соотношение
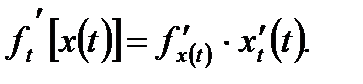 (3.21)
(3.21)
На самом деле, так как  дифференцируема в точке
дифференцируема в точке 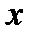 , то согласно определению 3.7 имеем
, то согласно определению 3.7 имеем
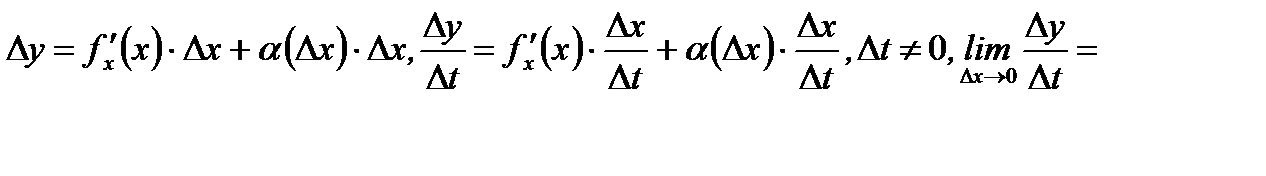
 (3.22)
(3.22)
С учетом того, что 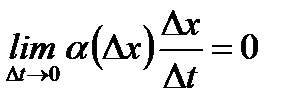 и
и 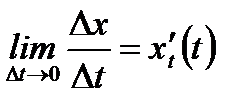 из (3.22) получим правило вычисления производной от сложной функции:
из (3.22) получим правило вычисления производной от сложной функции:
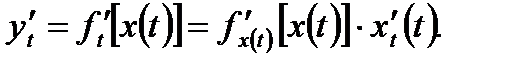 (3.23) Пользуясь (3.23), можно получить и следующие правила вычисления производной от гиперболических и степенно-показательной функций:
(3.23) Пользуясь (3.23), можно получить и следующие правила вычисления производной от гиперболических и степенно-показательной функций:
1.  (3.24)
(3.24)
2. 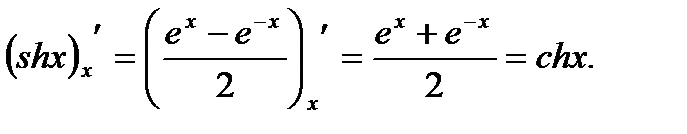 (3.25)
(3.25)
3. 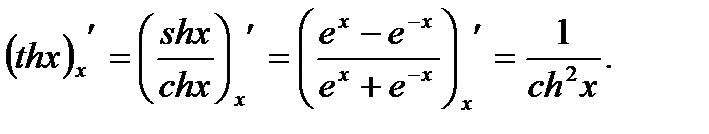 (3.26)
(3.26)
4.
| - |
| n |
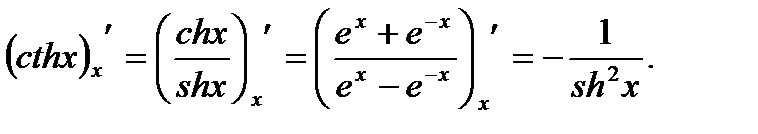 (3.27)
(3.27)
5. 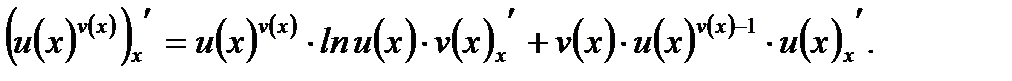 (3.28)
(3.28)
В случае, когда аргумент 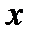 не зависит от других переменных, для производных и дифференциалов порядка выше первого можно получить следующие соотношения:
не зависит от других переменных, для производных и дифференциалов порядка выше первого можно получить следующие соотношения:
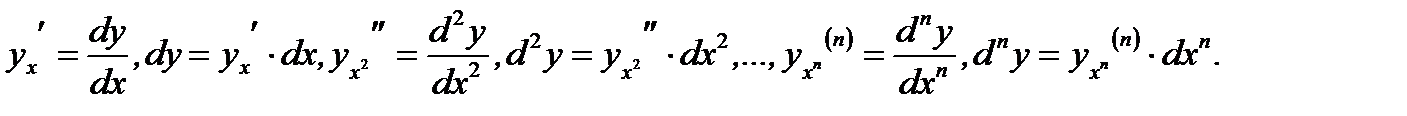 (3.29)
(3.29)
Если функция  задана в параметрическом виде, то есть
задана в параметрическом виде, то есть 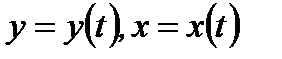 , то производную по
, то производную по 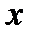 первого и второго порядков можно вычислить по ниже приведенным правилам
первого и второго порядков можно вычислить по ниже приведенным правилам
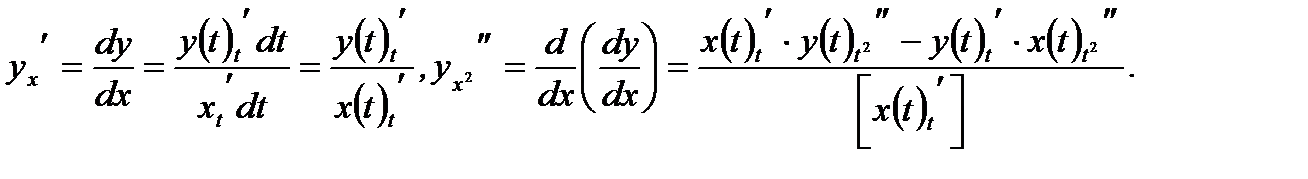 (3.30)
(3.30)
Если же невозможно найти явно  как функцию от
как функцию от  то есть, когда имеем неявно заданную функцию в виде
то есть, когда имеем неявно заданную функцию в виде 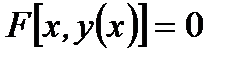 , то для нахождения производной от
, то для нахождения производной от  по
по 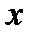 нужно просто от обеих частей выражения вычислить производную по
нужно просто от обеих частей выражения вычислить производную по 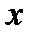 и потом решить полученное уравнение
и потом решить полученное уравнение 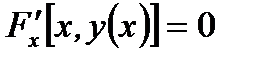 относительно
относительно 
Для некоторых элементарных функций можно получить формулы для вычисления
производной 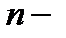 го порядка по
го порядка по 
1. 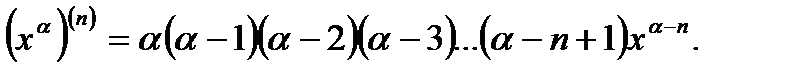 2.
2. 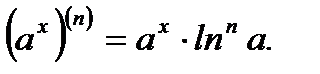 (3.31)
(3.31)
3. 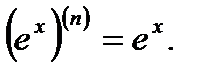 4.
4. 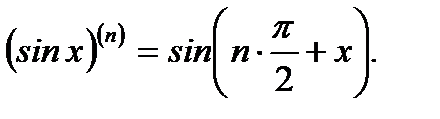 5.
5. 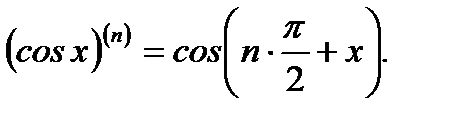 (3.32)
(3.32)
Ниже приведем формулу Лейбница для вычисления 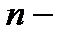 го порядка производной от произведения двух дифференцируемых функций
го порядка производной от произведения двух дифференцируемых функций 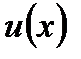 и
и 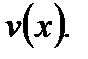 Она имеет вид
Она имеет вид
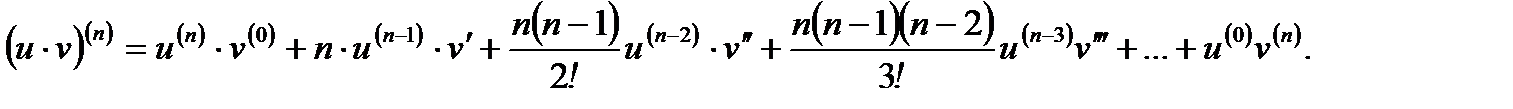 (3.33)
(3.33)
Пусть функции 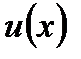 и
и  дифференцируемы в
дифференцируемы в 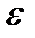 окрестности точки
окрестности точки 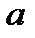 и
и 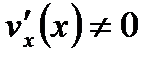 . 1. Если
. 1. Если 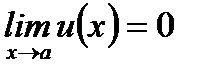 и
и 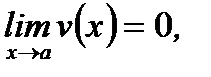 то есть частное
то есть частное 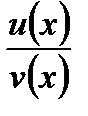 представляет собой неопределенность типа
представляет собой неопределенность типа 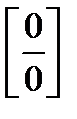 , то
, то
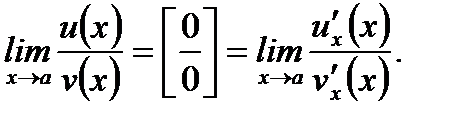 (3.34)
(3.34)
2. Если 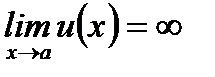 и
и  то есть частное
то есть частное 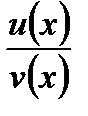 представляет собой неопределенность типа
представляет собой неопределенность типа 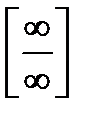 , то
, то
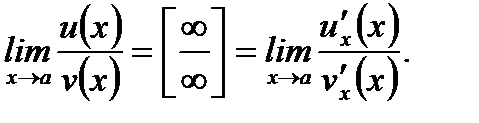 (3.35)
(3.35)
(3.34) и (3.35) называются правилами Лопиталя раскрытия неопределенностей типа 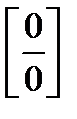 и
и  . Если же частное
. Если же частное 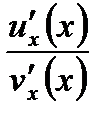 в точке
в точке 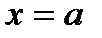 представляет собой неопределенность типа
представляет собой неопределенность типа 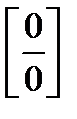 или
или  и функции
и функции 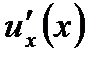 и
и  дифференцируемы в
дифференцируемы в 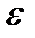 окрестности точки
окрестности точки 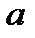 (
( 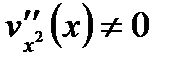 ), то следует применить еще раз правила Лопиталя. Отметим, что этот процесс можно продолжить, если удовлетворяются соответствующие условия для применения правил Лопиталя. В случаях неопределенностей типа
), то следует применить еще раз правила Лопиталя. Отметим, что этот процесс можно продолжить, если удовлетворяются соответствующие условия для применения правил Лопиталя. В случаях неопределенностей типа 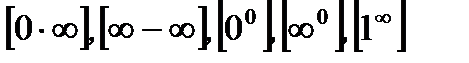 следует с помощью алгебраических преобразований перейти к неопределенности типа
следует с помощью алгебраических преобразований перейти к неопределенности типа 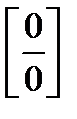 или
или  и потом применить правила Лопиталя.
и потом применить правила Лопиталя.
Дата добавления: 2018-11-25; просмотров: 574;
