Числовые последовательности.
Теория числовых последовательностей и функций одной переменной
Числовые последовательности.
3.1.1. Сходимость числовых последовательностей. Число 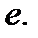
Определение 3.1.Говорим, что имеем числовую последовательность 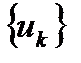 , если известно правило, согласно которому каждому
, если известно правило, согласно которому каждому 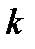 из множества натуральных чисел
из множества натуральных чисел 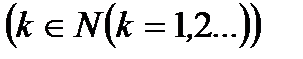 соответствует определенное число
соответствует определенное число 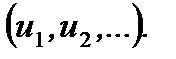 Полученный ряд занумерованных чисел называется числовой последовательностью.
Полученный ряд занумерованных чисел называется числовой последовательностью.
Пример 3.1. 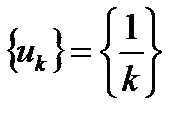 . При
. При 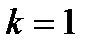
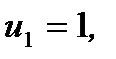 при
при 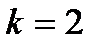
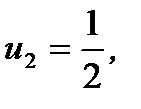 при
при 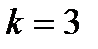
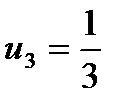 и так далее.
и так далее.
Получаем числовую последовательность 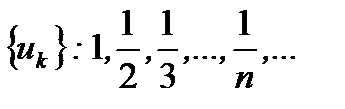 .
.
Пример 3.2. 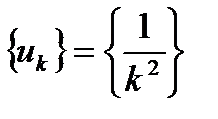 . При
. При 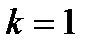
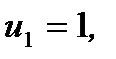 при
при 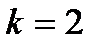
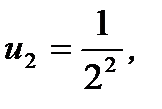 при
при 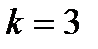
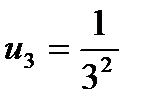 и так далее. Получаем числовую последовательность
и так далее. Получаем числовую последовательность 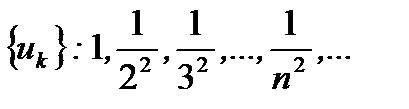 .
.
Пример 3.3. 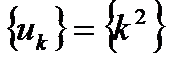 . При
. При 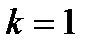
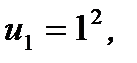 при
при 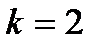
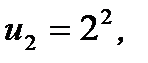 при
при 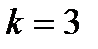
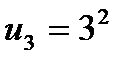 и так далее. Получаем числовую последовательность
и так далее. Получаем числовую последовательность 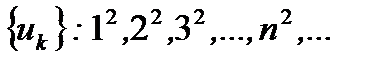 .
.
Пример 3.4. 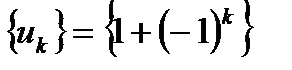 . При
. При 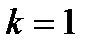
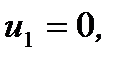 при
при 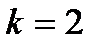
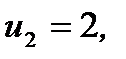 при
при 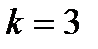
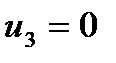 и так далее. Получаем числовую последовательность
и так далее. Получаем числовую последовательность 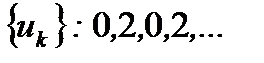 .
.
Видно, что в приведенных примерах есть последовательности, у которых каждый последующий элемент меньше предыдущего (последовательности убывают), и есть последовательность, у которой каждый последующий элемент больше предыдущего (последовательность возрастает). Помимо этого есть последовательность, которая не убывает и не возрастает. Основной вопрос в теории числовых последовательностей состоит в выяснении поведения последовательности, когда номер 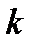 бесконечно растет
бесконечно растет 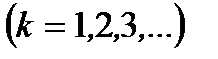 или
или 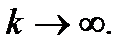 Очевидно, что примеры 1 и 2 являются бесконечно малыми последовательностями, т.е.
Очевидно, что примеры 1 и 2 являются бесконечно малыми последовательностями, т.е. 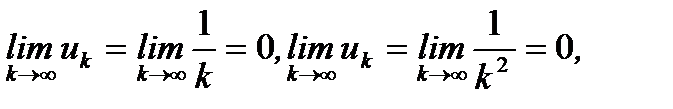 а пример 3 является бесконечно большой последовательностью, т.е.
а пример 3 является бесконечно большой последовательностью, т.е. 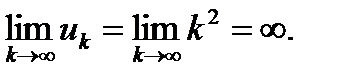 Отметим, что последовательность в примере 4 не имеет предела. Если при
Отметим, что последовательность в примере 4 не имеет предела. Если при 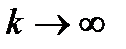 числовая последовательность стремится к конечному числу, то она сходится, а если стремится к бесконечности или нет предела, то она расходится.
числовая последовательность стремится к конечному числу, то она сходится, а если стремится к бесконечности или нет предела, то она расходится.
Определение 3.2.Число 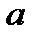 называется пределом последовательности
называется пределом последовательности 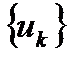 при
при 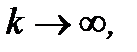 если для произвольного положительного числа
если для произвольного положительного числа 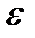 (это число выбираем заранее) можно указать (или существует) номер
(это число выбираем заранее) можно указать (или существует) номер 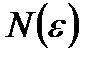 такой, что при
такой, что при 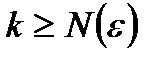 следует неравенство
следует неравенство 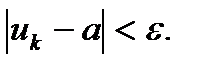 Это определение на языке символики имеет вид:
Это определение на языке символики имеет вид:
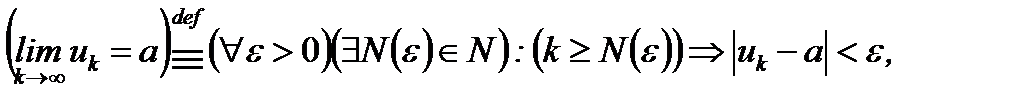
где def означает «определяется»,  – для произвольного,
– для произвольного, 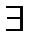 – существует, : – такое, что.
– существует, : – такое, что.
Последнее неравенство эквивалентно неравенствам: 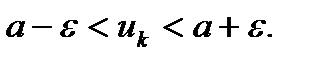 То есть число
То есть число 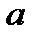 является пределом последовательности
является пределом последовательности 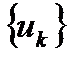 , если, начиная с номера
, если, начиная с номера 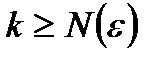 все элементы последовательности попадают в
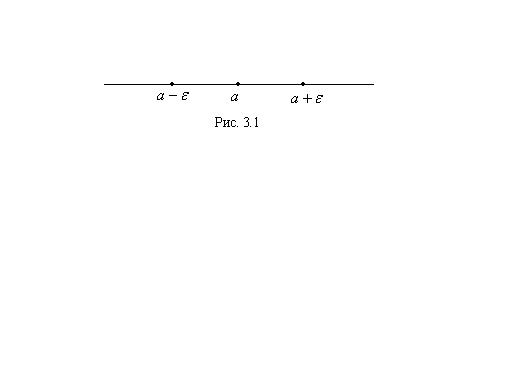
все элементы последовательности попадают в 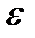 окрестность точки
окрестность точки 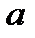 (рис. 3.1).
(рис. 3.1).
Можно доказать, что если 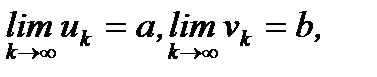 то имеют место следующие соотношения:
то имеют место следующие соотношения:
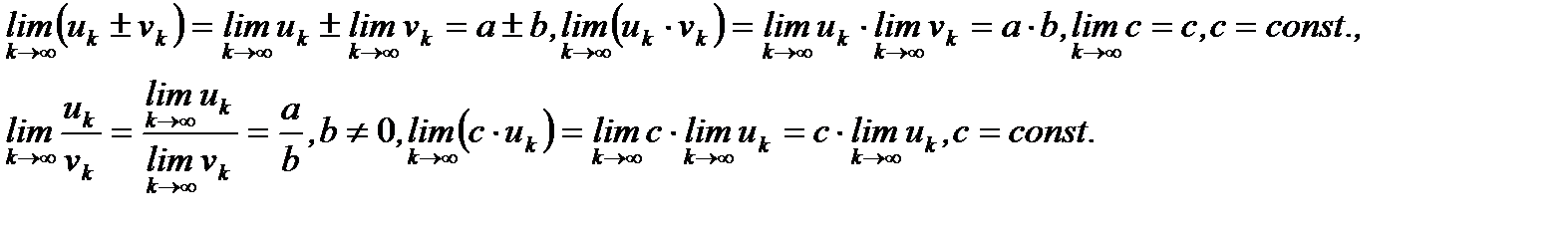
Рассмотрим числовую последовательность 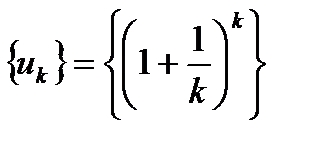 и выясним поведение этой
и выясним поведение этой
последовательности при 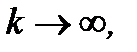 или другими словами вычислим предел
или другими словами вычислим предел 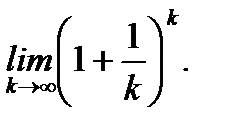 Исследования показали, что данная последовательность возрастает
Исследования показали, что данная последовательность возрастает 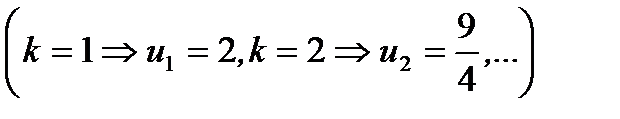 , но ограничена сверху числом 3. По теореме Вейерштрасса такая последовательность сходится. Предел последовательности обозначен через
, но ограничена сверху числом 3. По теореме Вейерштрасса такая последовательность сходится. Предел последовательности обозначен через  Итак имеем
Итак имеем 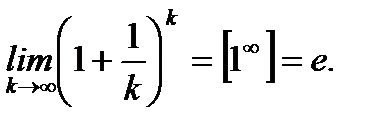 Здесь впервые встречаемся с понятием неопределенности типа единица в степени бесконечность. Отметим, что предел рассматриваемой последовательности не равен единице, а равен числу
Здесь впервые встречаемся с понятием неопределенности типа единица в степени бесконечность. Отметим, что предел рассматриваемой последовательности не равен единице, а равен числу 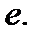 Отметим также, что
Отметим также, что 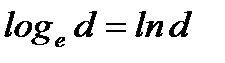 и последнее называется натуральным логарифмом. В математическом анализе помимо указанной выше неопределенности будут встречаться и неопределенности других типов:
и последнее называется натуральным логарифмом. В математическом анализе помимо указанной выше неопределенности будут встречаться и неопределенности других типов: 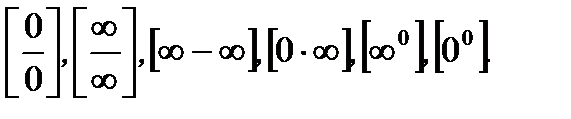
Дата добавления: 2018-11-25; просмотров: 606;
