Числовые ряды с произвольными членами. Достаточные признаки сходимости.
Если члены Uk ряда 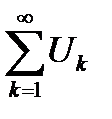 имеют произвольные знаки, то ряд
имеют произвольные знаки, то ряд 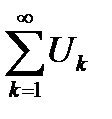 называется рядом с произвольными членами.
называется рядом с произвольными членами.
Определение 6.7. Ряд с произвольными членами 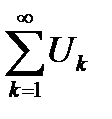 называется абсолютно сходящимся, если сходится ряд
называется абсолютно сходящимся, если сходится ряд 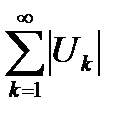 .
.
Теорема 6.14. Из сходимости ряда 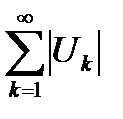 следует сходимость ряда
следует сходимость ряда 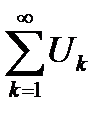 .
.
Доказательство. По условию теоремы ряд 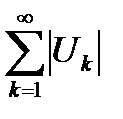 сходится. Согласно критерию Коши (см. теорему 6.1) это означает, что
сходится. Согласно критерию Коши (см. теорему 6.1) это означает, что
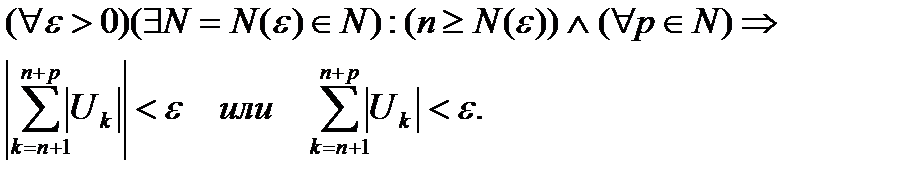 (6.30)
(6.30)
Оценим 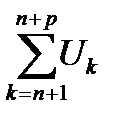 , пользуясь (6.30) и тем, что модуль суммы нескольких слагаемых не превосходит суммы их модулей. Имеем
, пользуясь (6.30) и тем, что модуль суммы нескольких слагаемых не превосходит суммы их модулей. Имеем
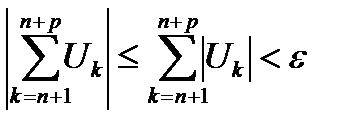 (6.31)
(6.31)
при 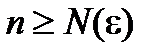 . А по критерию Коши (6.31) означает, что ряд
. А по критерию Коши (6.31) означает, что ряд 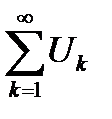 сходится.
сходится.
Теорема доказана.
Определение 6.8.Ряд 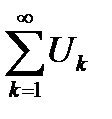 называется условно сходящимся, если он сходится, в то время, как соответствующий ряд из модулей
называется условно сходящимся, если он сходится, в то время, как соответствующий ряд из модулей 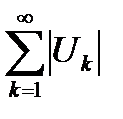 расходится.
расходится.
Теорема 6.15. (теорема Римана). Если ряд 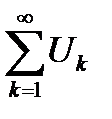 с произвольными членами сходится условно, то каково бы ни было наперед взятое число
с произвольными членами сходится условно, то каково бы ни было наперед взятое число 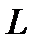 , можно так переставить члены этого ряда, чтобы преобразованный ряд сходился к числу
, можно так переставить члены этого ряда, чтобы преобразованный ряд сходился к числу 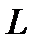 .
.
Теорема 6.16. Если данный ряд 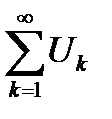 с произвольными членами сходится абсолютно, то любой ряд, полученный из данного ряда посредством некоторой перестановки членов, также сходится абсолютно и имеет ту же сумму, что и данный ряд.
с произвольными членами сходится абсолютно, то любой ряд, полученный из данного ряда посредством некоторой перестановки членов, также сходится абсолютно и имеет ту же сумму, что и данный ряд.
Пример 6.5. Исследуем на сходимость ряд с произвольными членами 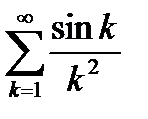 .
.
Решение. Составим ряд из модулей 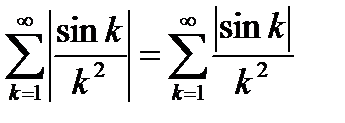 .
.
Этот ряд является рядом с положительными членами. Так как
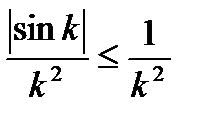 , (6.32)
, (6.32)
а ряд 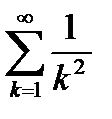 сходится (см. пункт 6.3), то по первому признаку сравнения (см. теорему 6.7) ряд
сходится (см. пункт 6.3), то по первому признаку сравнения (см. теорему 6.7) ряд 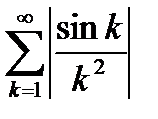 сходится. Тогда по теореме 6.14 исходный ряд также сходится.
сходится. Тогда по теореме 6.14 исходный ряд также сходится.
Ответ:Исходный ряд сходится абсолютно.
Определение 6.9. Ряд 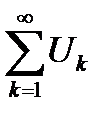 называется знакочередующимся, если члены этого ряда поочередно имеют то положительные, то отрицательные знаки. Знакочередующийся ряд обозначается так
называется знакочередующимся, если члены этого ряда поочередно имеют то положительные, то отрицательные знаки. Знакочередующийся ряд обозначается так
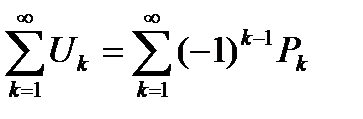 , (6.33)
, (6.33)
где 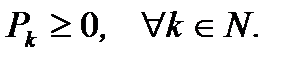
Теорема 6.17. (достаточный признак Лейбница условной сходимости знакочередующегося ряда).
Если члены знакочередующегося ряда
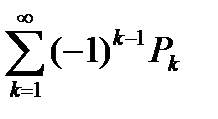 , (6.34)
, (6.34)
будучи взятые по модулю, образуют невозрастающую бесконечно малую последовательность, то есть удовлетворяют следующим условиям
а) 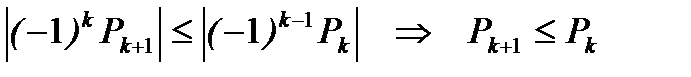 , (6.35)
, (6.35)
б) 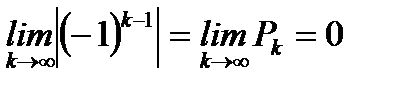 , (6.36)
, (6.36)
то знакочередующийся ряд 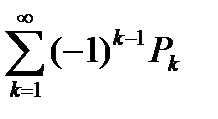 сходится.
сходится.
Доказательство. Частичная сумма ряда (6.34) четного порядка имеет вид
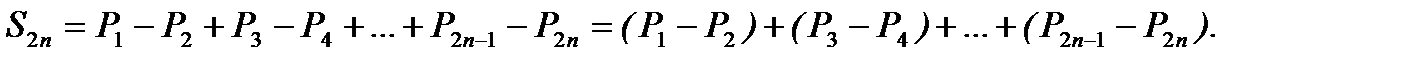 (6.37)
(6.37)
Согласно условию (6.35)
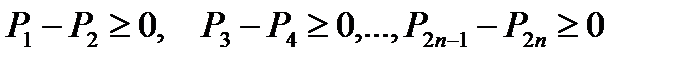 .
.
Тогда очевидно, что 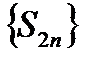 при
при 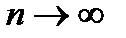 не убывает. С другой стороны, выражение (6.37) для
не убывает. С другой стороны, выражение (6.37) для 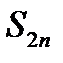 можно представить в виде
можно представить в виде
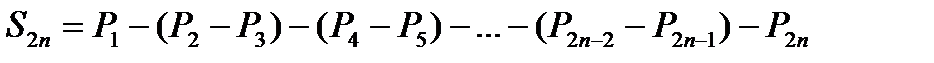 .
.
Так как 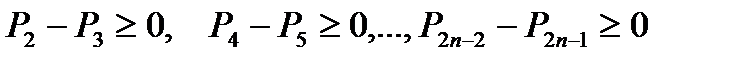 , то ясно, что для
, то ясно, что для 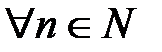 справедливо неравенство
справедливо неравенство 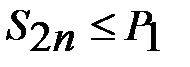 . Таким образом, оказывается, что последовательность частичных сумм четного порядка
. Таким образом, оказывается, что последовательность частичных сумм четного порядка 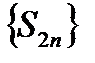 не убывает и ограничена сверху. Как известно, такая последовательность сходится к некоторому числу
не убывает и ограничена сверху. Как известно, такая последовательность сходится к некоторому числу 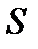
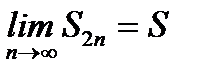 . (6.38)
. (6.38)
Частичная сумма ряда (6.34) нечетного порядка 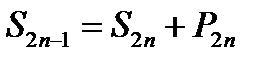 . В этом равенстве перейдем к пределу при
. В этом равенстве перейдем к пределу при 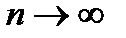 . Имеем
. Имеем
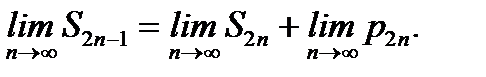 (6.39)
(6.39)
Учитывая (6.38) и второе условие теоремы, из (6.39) получим
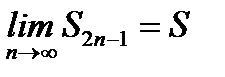 . (6.40)
. (6.40)
Таким образом, как следует из (6.38) и (6.40), 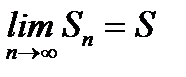 , то есть исходный знакочередующийся ряд (6.34) сходится.
, то есть исходный знакочередующийся ряд (6.34) сходится.
Теорема доказана.
Дата добавления: 2018-11-25; просмотров: 765;
