имеет конечное число точек экстремума.
Тогда во всякой точке этого сегмента, в которой непрерывна, функцию можно разложить в ряд Фурье (6.87), который в каждой точке сегмента сходится к . Если есть точка разрыва , то сумма ряда Фурье в этой точке имеет вид
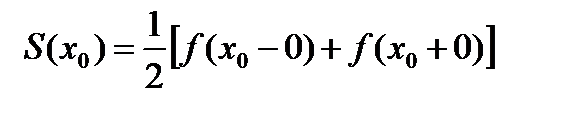 ,
,
а 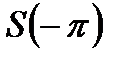 и
и 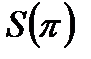 определяются так
определяются так
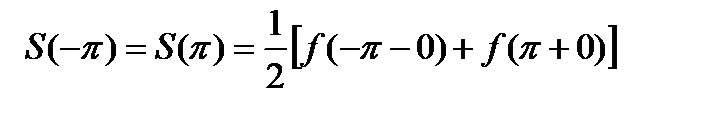 .
.
При вычислении определенного интеграла мы уже отмечали, что вычисления упрощаются в случае интегрирования четной и нечетной функции.
Если на сегменте 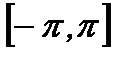 функция
функция 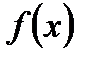 четная, то все ее коэффициенты Фурье
четная, то все ее коэффициенты Фурье 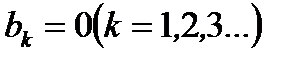 и ее ряд Фурье будет содержать только косинусы. Если функция нечетная, то все ее коэффициенты Фурье
и ее ряд Фурье будет содержать только косинусы. Если функция нечетная, то все ее коэффициенты Фурье 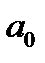 и
и 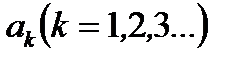 раны нулю и ее ряд Фурье будет содержать только синусы. В том случае, если функция задана на половине периода, то «доопределив» ее на другой половине периода как четную, можно получить ее разложение в ряд Фурье, в котором коэффициенты
раны нулю и ее ряд Фурье будет содержать только синусы. В том случае, если функция задана на половине периода, то «доопределив» ее на другой половине периода как четную, можно получить ее разложение в ряд Фурье, в котором коэффициенты 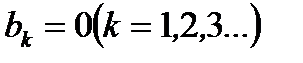 будут равны 0. Если такую функцию доопределить как нечетную, можно получить ее разложение в ряд Фурье, в котором коэффициенты
будут равны 0. Если такую функцию доопределить как нечетную, можно получить ее разложение в ряд Фурье, в котором коэффициенты 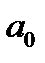 и
и 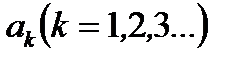 будут равны 0.
будут равны 0.
Пример 6.29. Разложить функцию 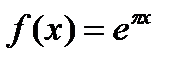 , заданную в промежутке
, заданную в промежутке 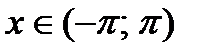 в ряд Фурье.
в ряд Фурье.
Решение. Согласно формулам (6.88) имеем
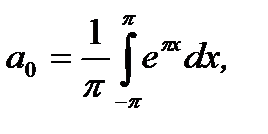
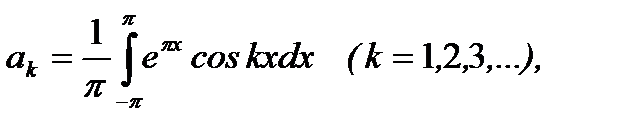
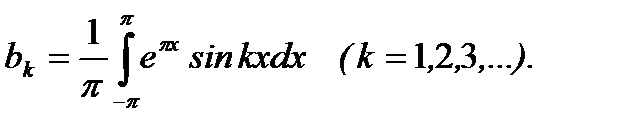
Проведя вычисление соответсвующих интегралов, получим
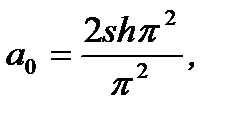
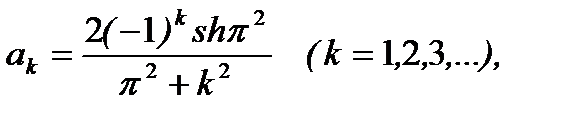
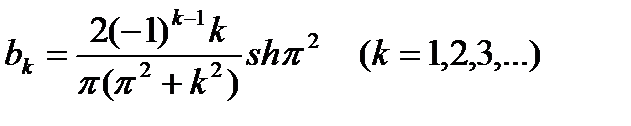 . (6.92)
. (6.92)
Подставляя (6.92) в (6.87), получим ряд Фурье заданной функции в виде
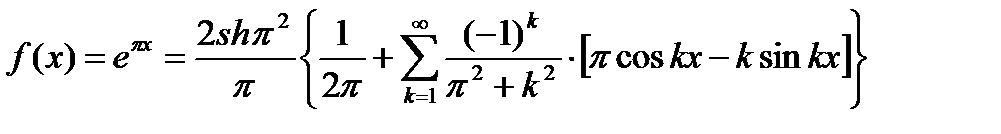 .
.
Пример 6.30. Разложить в ряд Фурье по синусам функцию 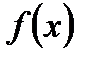 , определяемую равенствами
, определяемую равенствами
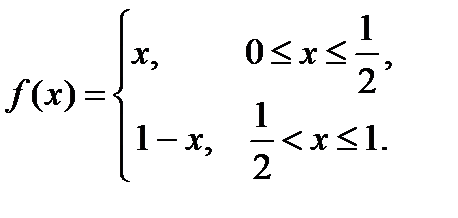 (6.93)
(6.93)
Решение.Согласно (6.90) имеем
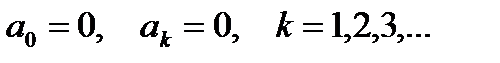 , (6.94)
, (6.94)
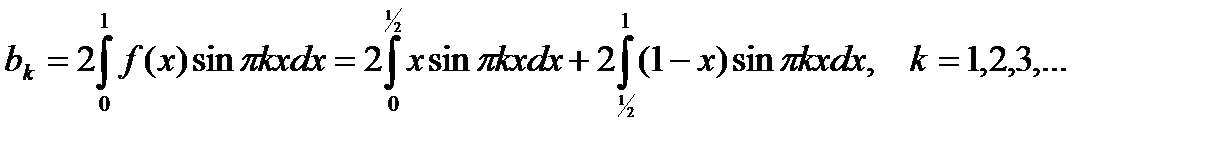 .
.
Полагая 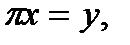 получим
получим
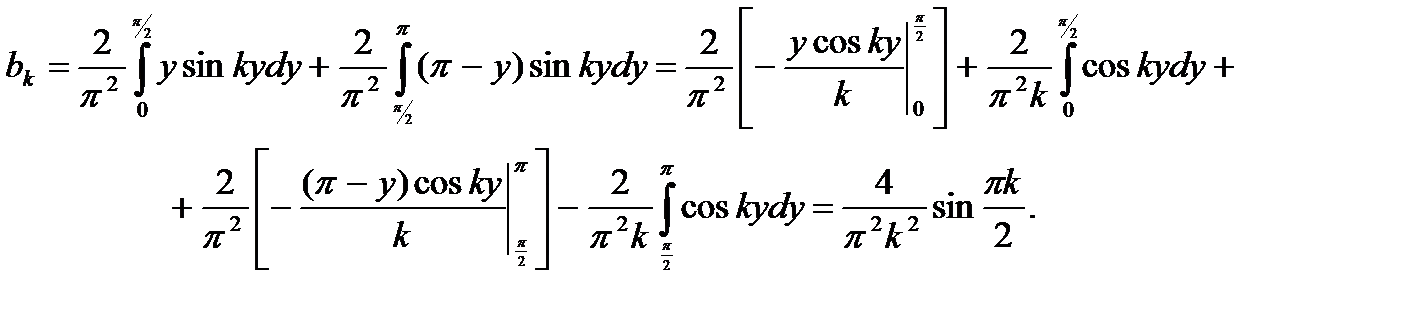 (6.95)
(6.95)
Тогда из (6.87) с учетом (6.94) и (6.95) получим
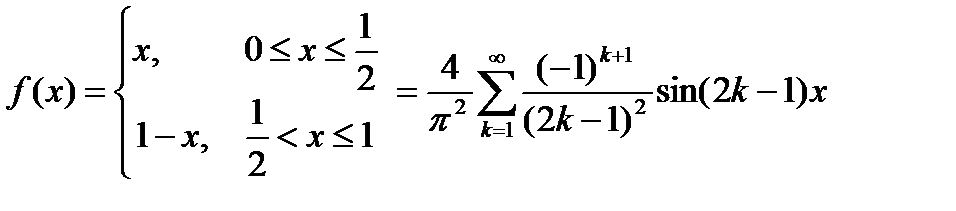 .
.
Пример 6.31. Разложить функцию 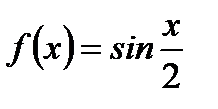 , заданную в промежутке
, заданную в промежутке 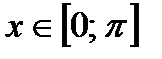 , в ряд Фурье по косинусам.
, в ряд Фурье по косинусам.
Решение.Доопределив заданную функцию до 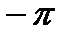 четным образом и вычисляя коэффициенты ряда Фурье, получим
четным образом и вычисляя коэффициенты ряда Фурье, получим
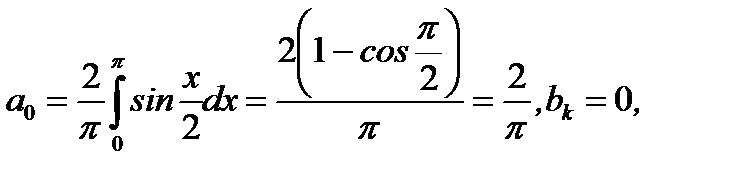 (6.96)
(6.96) 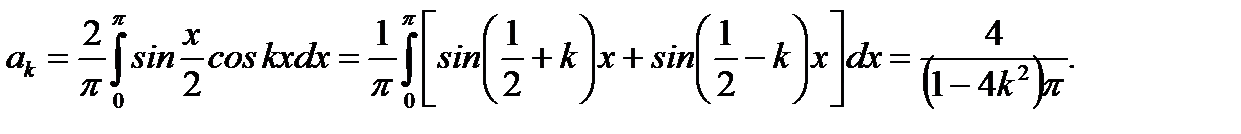 (6.97)
(6.97)
Подставляя (6.96) и (6.97) в (6.87), получим
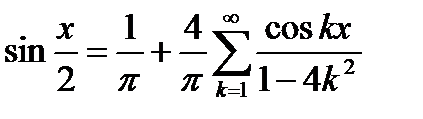 .
.
Пример 6.32. Разложить функцию 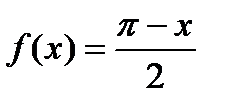 , заданную в промежутке
, заданную в промежутке 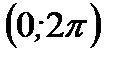 в ряд Фурье.
в ряд Фурье.
Решение.Заметим, что для произвольной функции 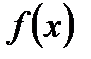 , имеющей период
, имеющей период 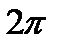 , величина интеграла
, величина интеграла 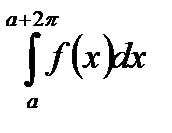 по промежутку длины
по промежутку длины 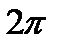 не зависит от
не зависит от 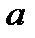 . Тогда, согласно этому, коэффициенты Фурье в этом случае есть
. Тогда, согласно этому, коэффициенты Фурье в этом случае есть
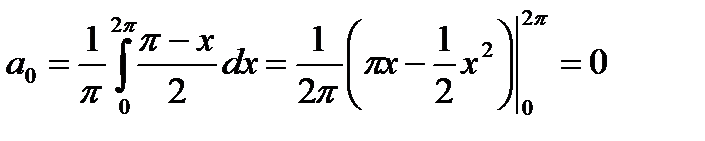 , (6.98)
, (6.98)
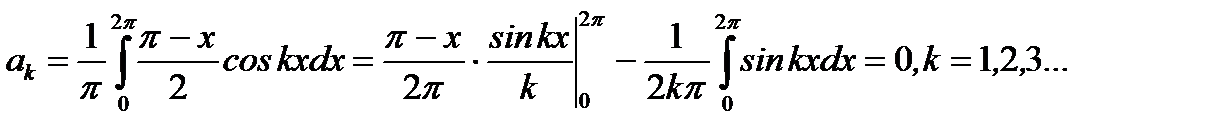 , (6.99)
, (6.99)
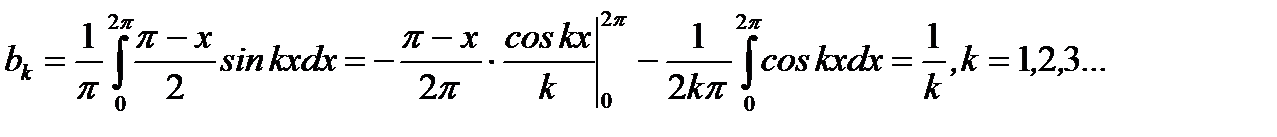 . (6.100)
. (6.100)
Таким образом, согласно (6.87) получим 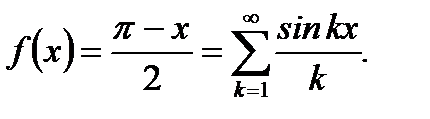
Задачи с ответами.
6.3.1. Пользуясь определением сходимости ряда, найти сумму ряда 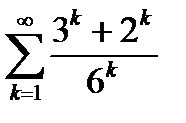 .
.
Ответ: 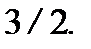
6.3.2. Исследовать числовой ряд с положительными членами 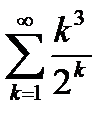 на сходимость.
на сходимость.
Ответ:сходится.
6.3.3. Исследовать числовой ряд с положительными членами 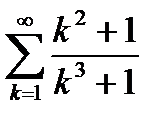 на сходимость.
на сходимость.
Ответ:расходится.
6.3.4. Исследовать числовой ряд с произвольными членами 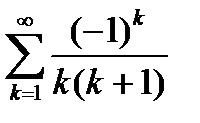 на сходимость.
на сходимость.
Ответ:сходится абсолютно.
6.3.5. Исследовать числовой ряд с произвольными членами 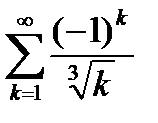 на сходимость.
на сходимость.
Ответ:сходится условно.
6.3.6. Найти радиус сходимости и область сходимости степенного ряда 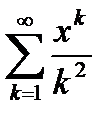 .
.
Ответ: 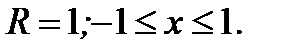
6.3.7. Найти радиус сходимости и область сходимости степенного ряда 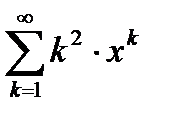 .
.
Ответ: 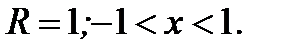
6.3.8. Вычислить 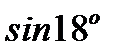 с точностью до
с точностью до 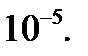
Ответ: 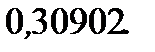
6.3.9. Разложить в ряд Тейлора по степеням х функцию 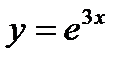 и указать область сходимости.
и указать область сходимости.
Ответ: 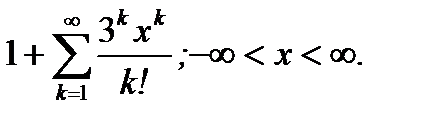
6.3.10. Разложить в ряд Тейлора по степеням х функцию 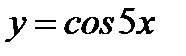 и указать область сходимости.
и указать область сходимости.
Ответ: 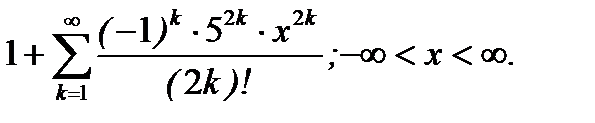
6.3.11. Вычислить 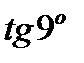 с точностью до
с точностью до 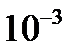 .
.
Ответ: 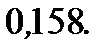
6.3.12. Разложить в ряд Фурье функцию 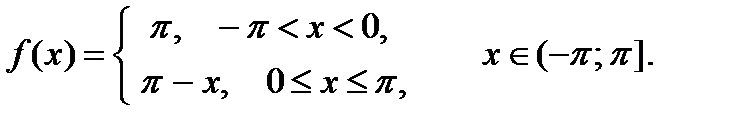
Ответ: 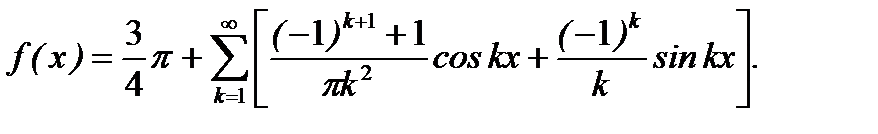
6.3.13. Разложить в ряд Фурье функцию 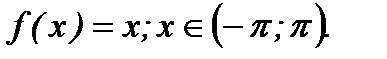
Ответ: 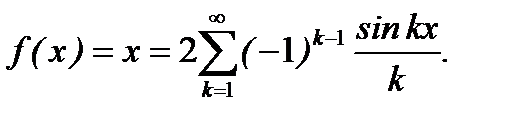
6.3.14. Разложить в ряд Фурье функцию 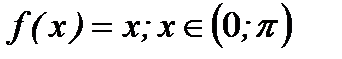 по косинусам.
по косинусам.
Ответ: 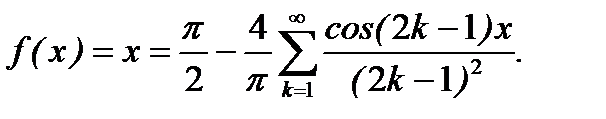
6.3.15. Разложить в ряд Фурье функцию 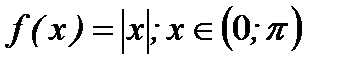 по синусам.
по синусам.
Ответ: 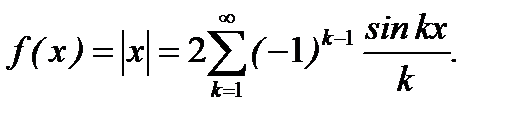
Дата добавления: 2018-11-25; просмотров: 519;
