Доказательство:обозначим через и п-ые частичные суммы рядов и .
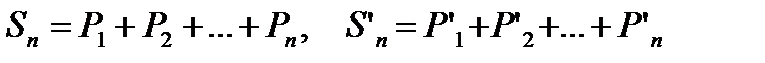 . (6.18)
. (6.18)
По условию теоремы 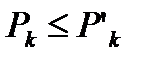 . Тогда
. Тогда
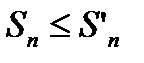 . (6.19)
. (6.19)
Если ряд 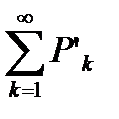 сходится, то по теореме 6.6
сходится, то по теореме 6.6 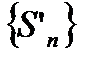 ограничена. Но тогда согласно (6.19)
ограничена. Но тогда согласно (6.19) 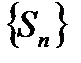 также ограничена. Следовательно, по теореме 6.6
также ограничена. Следовательно, по теореме 6.6 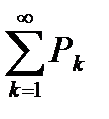 также сходится. А если ряд
также сходится. А если ряд 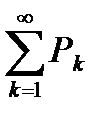 расходится, то по теореме 6.6
расходится, то по теореме 6.6 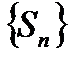 не ограничена, откуда следует, что
не ограничена, откуда следует, что 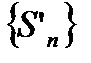 также не ограничена. Последнее, согласно теореме 6.6 означает, что ряд
также не ограничена. Последнее, согласно теореме 6.6 означает, что ряд 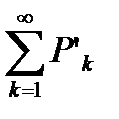 расходится.
расходится.
Теорема доказана.
Следствие теоремы 6.7 (признак сравнения в предельной форме).
Если 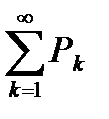 является рядом с положительными членами
является рядом с положительными членами 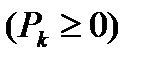 , а
, а 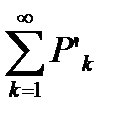 – со строго положительными членами
– со строго положительными членами 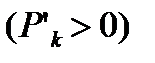 и существует конечный предел
и существует конечный предел
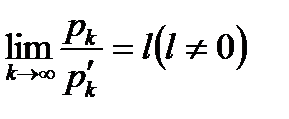 (6.20)
(6.20)
то из сходимости ряда 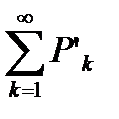 следует сходимость ряда
следует сходимость ряда 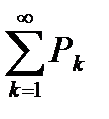 , а из расходимости ряда
, а из расходимости ряда 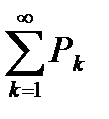 следует расходимость ряда
следует расходимость ряда 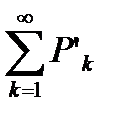 .
.
Теорема 6.8. Второй признак сравнения.
Пусть имеем два ряда 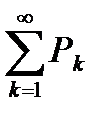 и
и 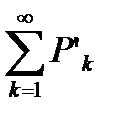 со строго положительными членами
со строго положительными членами 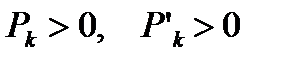 . Если для всех номеров к справедливо неравенство
. Если для всех номеров к справедливо неравенство
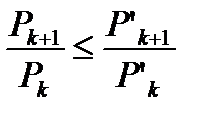 ,
,
то из сходимости ряда 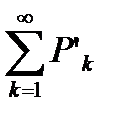 следует сходимость ряда
следует сходимость ряда 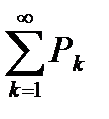 , а из расходимости ряда
, а из расходимости ряда 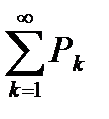 следует расходимость ряда
следует расходимость ряда 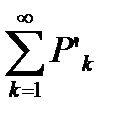 .
.
Теорема 6.9. Признак Даламбера.
Пусть дан ряд с положительными членами 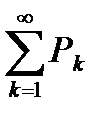 , причем хотя бы начиная с
, причем хотя бы начиная с 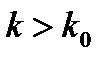 все
все 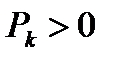 .
.
1. Если для всех номеров к, или по крайней мере начиная с некоторого номера 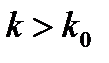 между членами ряда
между членами ряда 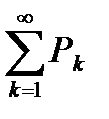 выполняется неравенство
выполняется неравенство
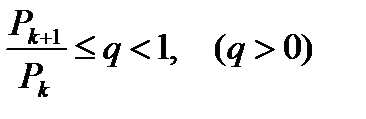 , (6.21)
, (6.21)
то ряд 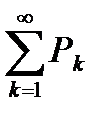 сходится.
сходится.
2. Если 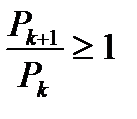 , начиная хотя бы с некоторого
, начиная хотя бы с некоторого 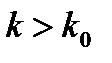 , то ряд
, то ряд 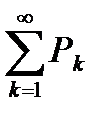 расходится.
расходится.
Доказательство.Для доказательства первой части теоремы 6.9 положим 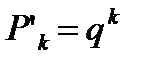 , где
, где 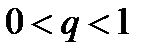 , и заметим, что ряд
, и заметим, что ряд 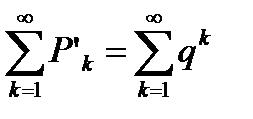 сходится согласно рассмотренному в пункте 6.2 второму примеру. Тогда
сходится согласно рассмотренному в пункте 6.2 второму примеру. Тогда
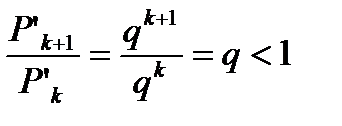 (6.22)
(6.22)
или
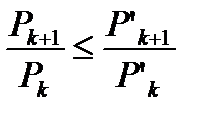 . (6.23)
. (6.23)
Так как ряд 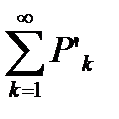 сходится, то по теореме 6.8 ряд
сходится, то по теореме 6.8 ряд 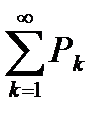 также сходится.
также сходится.
Для доказательства второй части этой теоремы положим 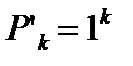 и заметим, что ряд
и заметим, что ряд 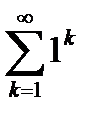 расходится согласно рассмотренному в пункте 6.2 первому примеру. Тогда
расходится согласно рассмотренному в пункте 6.2 первому примеру. Тогда
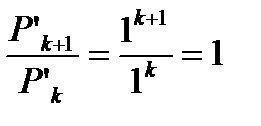 (6.24)
(6.24)
и
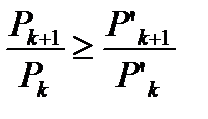 (6.25)
(6.25)
Так как ряд 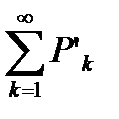 =
= 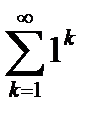 расходится, то по теореме 6.8 ряд
расходится, то по теореме 6.8 ряд 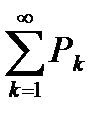 также расходится.
также расходится.
Теорема доказана.
Следствие теоремы 6.9 (признак Даламбера в предельной форме).
Если 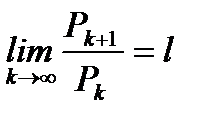 , то при l<1 ряд
, то при l<1 ряд 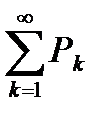 сходится, при l>1 ряд
сходится, при l>1 ряд 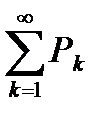 расходится, а при l=1 вопрос о сходимости ряда остается открытым.
расходится, а при l=1 вопрос о сходимости ряда остается открытым.
Теорема 6.10. Радикальный признак Коши.
Пусть дан ряд 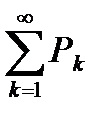 с положительными членами.
с положительными членами.
1. Если для всех номеров 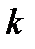 или, по крайней мере, начиная с некоторого номера
или, по крайней мере, начиная с некоторого номера 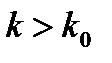 выполняется неравенство
выполняется неравенство
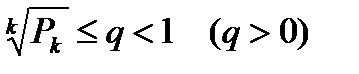 , (6.26)
, (6.26)
то ряд 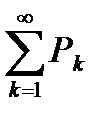 сходится.
сходится.
2. Если 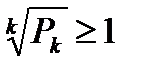 начиная хотя бы с некоторого
начиная хотя бы с некоторого 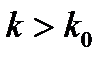 , то ряд
, то ряд 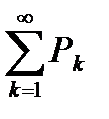 расходится.
расходится.
Отметим, что доказательство этого признака проводится аналогично доказательству признака Даламбера.
Следствие теоремы 6.10 (радикальный признак Коши в предельной форме).
Если 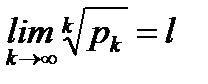 , то при l<1 ряд
, то при l<1 ряд 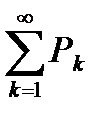 сходится, при l>1 ряд
сходится, при l>1 ряд 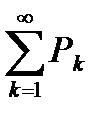 расходится, а при l=1 вопрос о сходимости ряда остается открытым.
расходится, а при l=1 вопрос о сходимости ряда остается открытым.
Теорема 6.11. Признак Раабе.
Пусть дан ряд с положительными членами 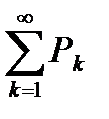 .
.
1. Если для всех номеров 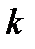 или, по крайней мере, начиная с некоторого номера
или, по крайней мере, начиная с некоторого номера 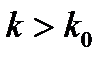 справедливо неравенство
справедливо неравенство
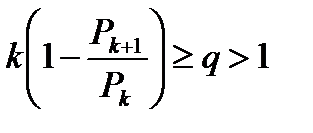 , (6.26)
, (6.26)
то ряд 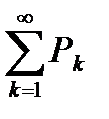 сходится.
сходится.
2. Если для всех номеров 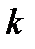 или начиная хотя бы с некоторого
или начиная хотя бы с некоторого 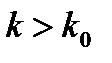
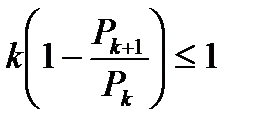 , то ряд
, то ряд 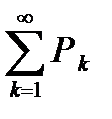 расходится.
расходится.
Следствие теоремы 6.11 (признак Раабе в предельной форме).
Если 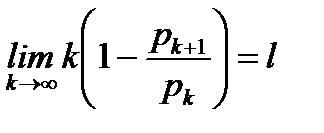 , то при l>1 ряд
, то при l>1 ряд 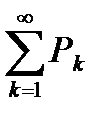 сходится, при l<1 ряд
сходится, при l<1 ряд 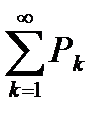 расходится, а при l=1 вопрос о сходимости ряда остается открытым.
расходится, а при l=1 вопрос о сходимости ряда остается открытым.
Теорема 6.12. Интегральный признак Коши – Маклорена.
Пусть дан ряд с положительными членами 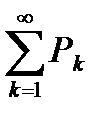 . Рассмотрим функцию f(x), удовлетворяющую на полупрямой
. Рассмотрим функцию f(x), удовлетворяющую на полупрямой 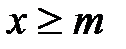 (
( 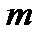 любой фиксированный номер) следующим условиям:
любой фиксированный номер) следующим условиям:
1. f(x) неотрицательна 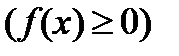 .
.
2. f(x) не возрастает 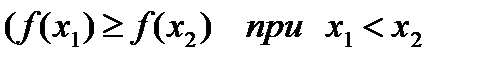 .
.
3. значения этой функции при 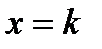 совпадают с членами данного ряда
совпадают с членами данного ряда 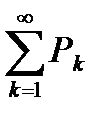
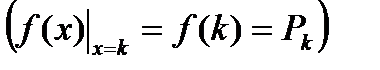 .
.
Если несобственный интеграл первого рода 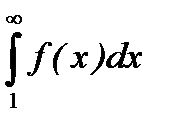 сходится, то ряд
сходится, то ряд 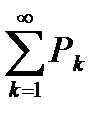 также сходится. Если несобственный интеграл
также сходится. Если несобственный интеграл 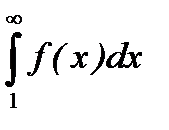 расходится, то ряд
расходится, то ряд 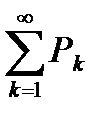 также расходится.
также расходится.
Ниже приведено геометрическое истолкование этой теоремы (см. рис. 6.1). Заметим, что несобственный интеграл 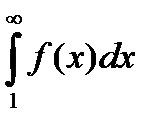 выражает площадь криволинейной трапеции.
выражает площадь криволинейной трапеции.
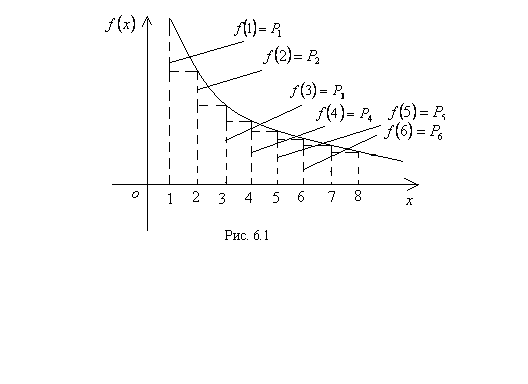
Исходный ряд можно переписать в виде
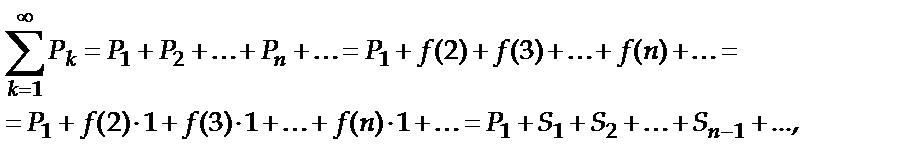
где 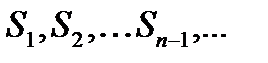 есть площади входящих в криволинейную трапецию прямоугольников. Если площадь криволинейной трапеции конечное число, то есть
есть площади входящих в криволинейную трапецию прямоугольников. Если площадь криволинейной трапеции конечное число, то есть 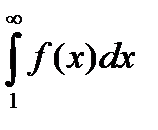 сходится, то подавно конечна площадь заключенной в ней ступенчатой фигуры, то есть ряд
сходится, то подавно конечна площадь заключенной в ней ступенчатой фигуры, то есть ряд 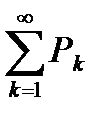 сходится. Если же площадь криволинейной трапеции бесконечно большая величина, то есть
сходится. Если же площадь криволинейной трапеции бесконечно большая величина, то есть 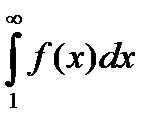 расходится, то площадь ступенчатой фигуры также бесконечно большая величина, то есть ряд
расходится, то площадь ступенчатой фигуры также бесконечно большая величина, то есть ряд 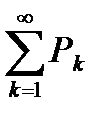 расходится.
расходится.
В качестве применения интегрального признака изучим поведение обобщенного гармонического ряда 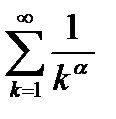 при
при 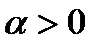 . Для этого рассмотрим по отдельности случаи
. Для этого рассмотрим по отдельности случаи 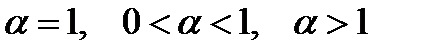 .
.
1. При 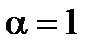 имеем ряд
имеем ряд 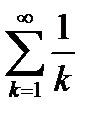 .
.
Тогда по интегральному признаку получим
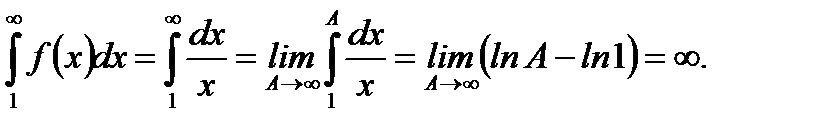 (6.27)
(6.27)
Отсюда следует, что ряд 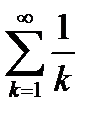 расходится (этот результат уже был получен критерием Коши в пункте 6.2).
расходится (этот результат уже был получен критерием Коши в пункте 6.2).
2. При 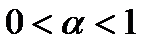 имеем ряд
имеем ряд 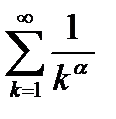 . Тогда по интегральному признаку получим
. Тогда по интегральному признаку получим 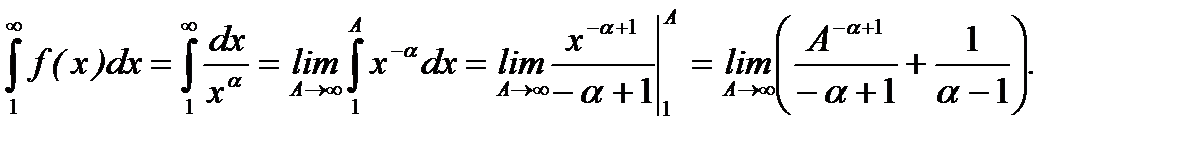 (6.28)
(6.28)
Очевидно, что при 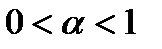 (6.28) стремится к бесконечности и ряд
(6.28) стремится к бесконечности и ряд 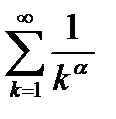 расходится, а при
расходится, а при 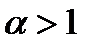 (6.28) стремится к конечному числу и ряд
(6.28) стремится к конечному числу и ряд 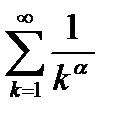 сходится.
сходится.
В итоге имеем 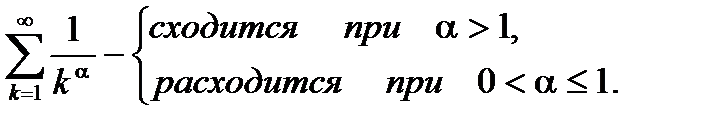
Теорема 6.13. Признак Гаусса.
Допустим, что для ряда 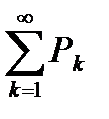 отношение
отношение 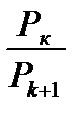 может быть представлено в виде
может быть представлено в виде
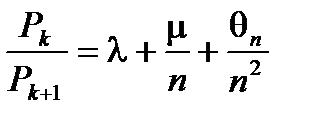 , (6.29)
, (6.29)
где l и m постоянные, а 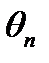 есть ограниченная величина (
есть ограниченная величина ( 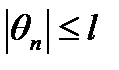 , l – конечное число). Тогда ряд
, l – конечное число). Тогда ряд 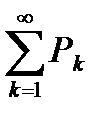 сходится, если
сходится, если 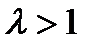 или если
или если 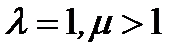 , и расходится, если
, и расходится, если 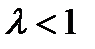 или
или 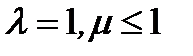 .
.
Дата добавления: 2018-11-25; просмотров: 526;
