Ряд и его частичные суммы. Сходящиеся и расходящиеся ряды.

Числовые и функциональные ряды. Ряды Фурье.

Числовые ряды.

Ряд и его частичные суммы. Сходящиеся и расходящиеся ряды.

Рассмотрим числовую последовательность

.

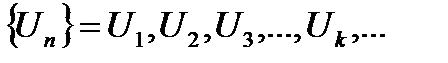Определение 6.1. Выражение вида

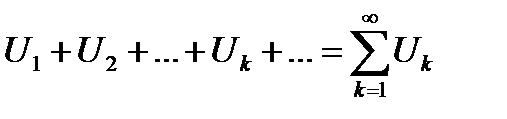(6.1)

называется числовым рядом, а 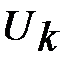называется общим членом этого ряда.

Определение 6.2. Сумма первых п членов данного ряда 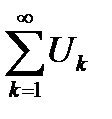называется п-ой частичной суммой этого ряда и обозначается через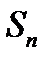

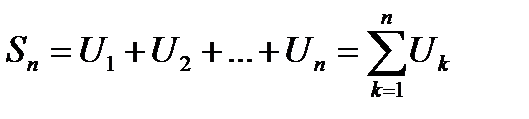. (6.2)

Определение 6.3. Ряд 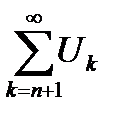называется п-ым остатком ряда 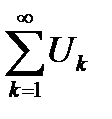и обозначается через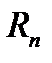

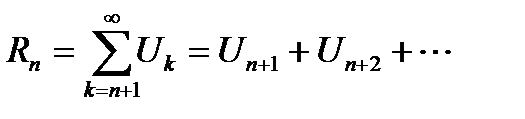. (6.3)

Определение 6.4. Ряд 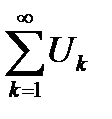называется сходящимся, если сходится последовательность его частичных сумм 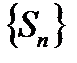, где

.

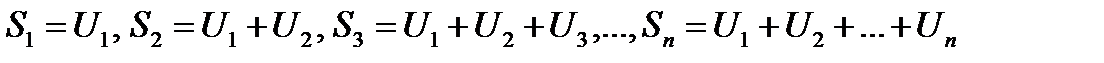При этом предел 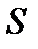последовательности частичных сумм 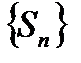называется суммой данного ряда

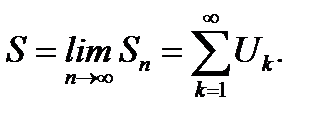(6.4)

Определение 6.5. Если предел последовательности частичных сумм 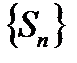стремится к плюс или минус бесконечности, или вовсе не существует, то ряд 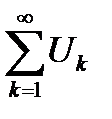называется расходящимся.

Теорема 6.1. Необходимое и достаточное условие сходимости ряда (критерий Коши).

Для того чтобы ряд 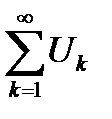сходился, необходимо и достаточно, чтобы для .

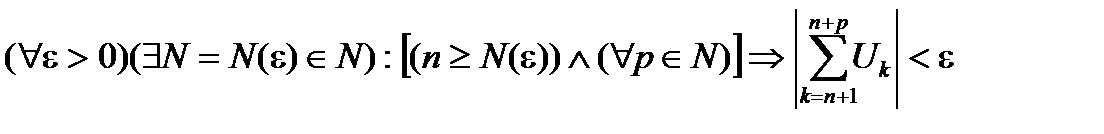Теорема 6.2. Если ряд 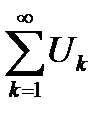сходится, то любой его остаток 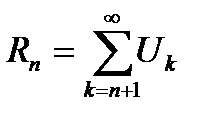сходится, причем является бесконечно малой величиной. Обратно, из сходимости остатка ряда 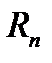вытекает сходимость данного ряда .

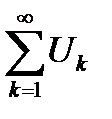Теорема 6.3. (необходимое условие сходимости ряда).

Для сходимости ряда 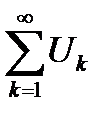необходимо, чтобы общий член ряда при 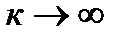стремился к нулю, то есть

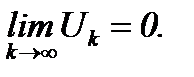(6.5)

Доказательство:по условию теоремы дано, что ряд 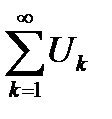сходится. Нужно доказать, что

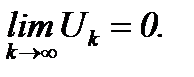
Обозначим сумму ряда через S

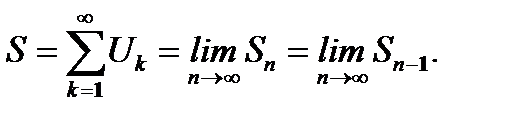(6.6)

Очевидно, что

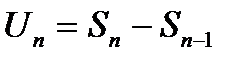. (6.7)

Перейдем в (6.7) к пределу при 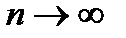и учтем (6.6). Тогда получим

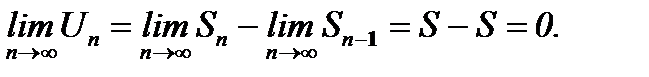(6.8)

Теорема доказана.

Замечание 6.1. Условие (6.5) является необходимым условием сходимости ряда и недостаточным. То есть, если ряд сходится, то обязательно его общий член стремится к нулю при 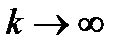. Но если известно, что 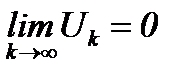, то отсюда не следует, что ряд сходится. Поэтому при исследовании любого ряда на сходимость желательно, прежде всего, проверить необходимое условие сходимости. Если 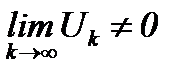, то заведомо ряд расходится. А если 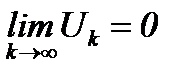, то дальше нужно исследовать на сходимость данный ряд, пользуясь достаточными условиями сходимости.

Ниже два основных свойства сходящихся рядов сформулируем в виде теорем (теоремы 6.4. и 6.5).

Теорема 6.4. Если ряд 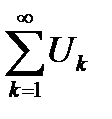сходится, то ряд 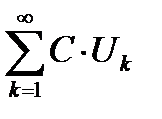, где 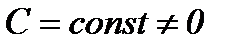также сходится и 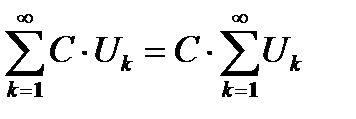(6.9)

Доказательство:обозначим 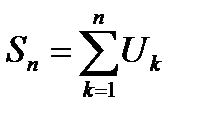и 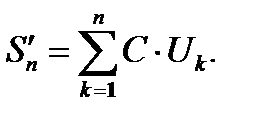Так как в верхних суммах конечное число слагаемых, то справедливо

.

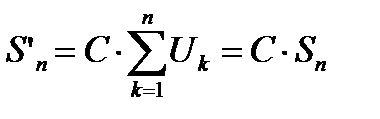Тогда

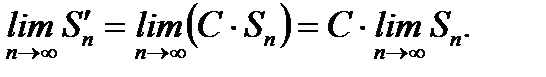(6.10)

По условию теоремы ряд 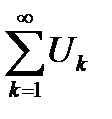сходится, то есть

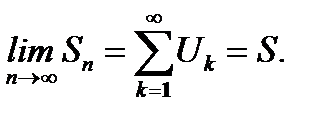(6.11)

где S сумма сходящегося ряда 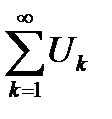. Учитывая (6.11) из (6.10) получим

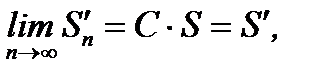
где 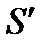сумма ряда .

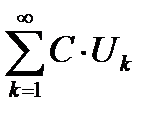Теорема доказана.

Теорема 6.5. Если ряды 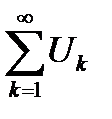и 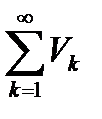сходятся, то ряд 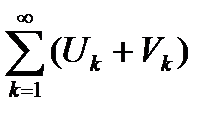также сходится и

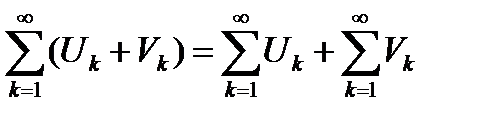. (6.12)

Замечание 6.2. Теорему 6.5 можно сформулировать и так: сходящиеся ряды можно складывать почленно.

Замечание 6.3. Доказательство теоремы 6.5 проводится аналогично доказательству теоремы 6.4.